1 вариант.
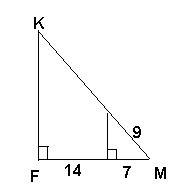
∠АСВ=∠СКМ. Найти х 2) Найти FK.
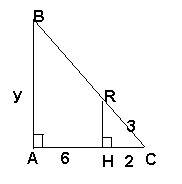
Найти у.
Диагонали трапеции АВСД с основаниями АВ и СД пересекаются в точке О. Найдите АВ, если ОВ=4 см, ОД=10 см, ДС=25 см.* Докажите, что два равносторонних треугольника подобны.II-вариант.
∠DAN=∠ARW. Найти RW 2) найти у
3) Найти FK.

Очевидно, что лучше как можно меньше совершать кругов. Но избежать их совсем не получится. Обозначим верхнюю точку D, а нижние A,B,C по часовой стрелке, начиная с самой левой. Ясно, что нам придется совершать круг внизу. Можно, конечно, пробегать по боковым граням (по их ребрам), но там получатся пробежки по одним и тем же ребрам по 2 раза, и количество таких пробежек больше одной.
Пробежка по низу ведется через боковое ребро. Допустим, это DA.
Тогда путь DA->AC->CB->BD->DA->AB->BC->CA (8). Это один из путей.
Можно путь DA->AC->CB->BA->AD->DC->CB->BD (8). Ещё один путь.
Вообще можно все представить как граф и его исследовать. Можно и просто, как я, но здесь минимальный такой путь равен 8.
Объяснение:a) Центр вписанной окружности треугольника - точка пересечения биссектрис.
AOP =BAO+ABO =A/2 +B/2 (внешний угол AOB)
CAP =CBP =B/2 (вписанные)
OAP =CAO +CAP =A/2 +B/2 =AOP
△APO - равнобедренный, PA=PO
Аналогично PC=PO
б) Центр T описанной окружности △APC лежит на серединном перпендикуляре к AC.
ATP =2ABP =B =60
△ATP - равнобедренный (TA=TP) с углом 60 - равносторонний.
AH - высота и медиана, PH =TP/2 =14/2 =7