
Вектор а пропорционален вектору, полученному векторным умножением векторов b и c.
Находим d = b x c по Саррюса:
i j k| i j
-4 -7 5| -4 -7
-8 -8 7| -8 -8 = -49i - 40j + 32k + 28j + 40i - 56k = -9i - 12j - 24k.
Получили вектор d, кратный вектору а:
d = (-9; -12; -24). его модуль равен:
|d| = √((-9)² + (-12)² + (-24)²) = √(81 + 144 + 576) = √801.
Подкоренное выражение кратно заданному 801/89 = 9.
То есть модуль а в 3 раза меньше.
Но ортогональным вектор а может иметь как в одном направлении, так и в противоположном.
Поэтому имеются 2 решения:
a = (-3; -4; -8),
(3; 4; 8).
Даны векторы k(-1;2), s(5;-12), c(2;x). Найдите: a)cos(∠k, s) ; b) число x, если k и c - коллинеарные; c) число x, если s и c - перпендикулярны.
Объяснение:
a)Косинус угла между векторами равен скалярному произведению этих векторов, деленному на произведение их длин.
Найдем длины векторов:
Длина вектора |k|=√( (-1)²+2²)=√(1 +4)=√5,
Длина вектора |s|=√( 5²+(-12)²)=√(25+144)=√169=13,
Скалярное произведение k*s=-1*5+2*(-12)=-5-24=-29
cos(∠k, s)= .
b) Два вектора коллинеарные ,если их координаты пропорциональны, значит для k(-1;2),c(2;x) : 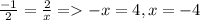 ;
;
c)Вектора перпендикулярны , если их скалярное произведение равно нулю :  ⇒ 12x=10 , x=
⇒ 12x=10 , x=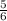 .
.
Возьмём треугольники MKT И PTS
1. MT=TS(по условию)
2. KT=TP(по условию)
3. Угол MTK= Углу PTS, так как они накрест лежащие. То Треугольник MKT=PTS