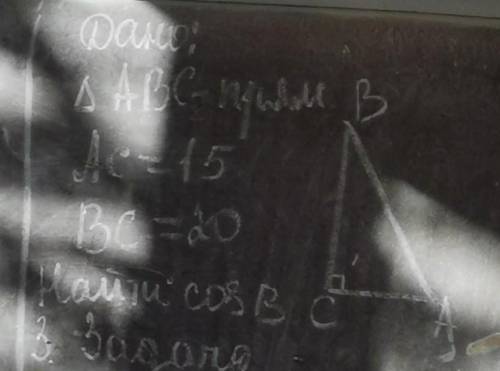
Для того, чтобы найти косинус острого угла прямоугольного треугольника нужно знать длину прилежащего катета и гипотенузы.
Прилежащий катет к ∠В - это ВС.
Гипотенуза - АВ (так как лежит против прямого угла).
АВ найдём по теореме Пифагора :
АВ² = ВС² + АС² = 20² + 15² = 400 + 225 = 625 ⇒ АС = √АС²= √625 = 25.
Тогда 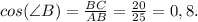
Решение
sin (pi/2+t)-cos(pi-t)+tg(pi-t)+ctg(5pi/2-t) = cost + cost - tgt + tgt =2cost
Объяснение:
sin (π/2 + t) - cos (π - t) + tg (π - t) + ctg (5π/2 - t). Для упрощения данного выражения используем формулы приведения. По формулам приведения: sin (π/2 + t) = cos t; cos (π - t) = – cos t; tg (π - t) = – tg t; ctg (5π/2 - t) = tg t. Таким образом, мы пришли к выражению: cos t - (– cos t) + (– tg t) + tg t = (раскроем скобки, если перед скобками стоит знак минус "-", то знак слагаемого в скобках необходимо поменять на противоположный) = cos t + cos t - tg t + tg t = (- tg t и tg t взаимно уничтожаются) = 2cos t. ответ: sin (π/2 + t) - cos (π - t) + tg (π - t) + ctg (5π/2 - t) = 2cos t.
косинус это отношение прилежащего катета ВС к гипотенузе АВ
cosB = ВС/AB
по т. Пифагора АВ = √ВС²+АС² = √20²+15² = √400+225 = √625 = 25
cosB = 20/25 = 4/5 = 0.8
cosB = 0.8