1. По теореме синусов:
a : sinA = b : sinB
sinB = b · sinA / a
sinB = 7 · sin60° / 10 = 7√3/20 ≈ 0,6062
∠B ≈ 37°
∠C = 180° - ∠A - ∠B ≈ 180° - 60° - 37° ≈ 83°
По теореме синусов:
a : sinA = c : sinC
c = a · sinC / sinA
c ≈ 10 · 0,9925 / 0,866 ≈ 11,5
2.
По теореме косинусов:
b² = a² + c² - 2ac·cosB
cosB = (a² + c² - b²) / (2ac)
cosB = (36 + 23,04 - 53,29) / 57,6
cosB ≈ 0,0998
∠B ≈ 83°
По теореме косинусов:
a² = b² + c² - 2bc·cosA
cosA = (b² + c² - a²) / (2bc)
cosA = (53,29 + 23,04 - 36) / 70,08
cosA ≈ 0,5755
∠A ≈ 54°
∠C = 180° - ∠B - ∠A ≈ 180° - 83° - 54° ≈ 43°
Объяснение:
Удачи)))
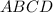 прямоугольная, то значит одна из её сторон перпендикулярна основаниям, а другая – наклонная. При этом есть две диагонали: одна идёт из прямого угла в тупой к короткому основанию, а другая – из прямого в острый к длинному основанию. Та диагональ, которая идёт к длинному основанию лежит напротив тупого угла трапеции, а значит она длиннее и короткого основания, и длинной боковой стороны (см. чертёж). Отсюда ясно, что указанная диагональ
прямоугольная, то значит одна из её сторон перпендикулярна основаниям, а другая – наклонная. При этом есть две диагонали: одна идёт из прямого угла в тупой к короткому основанию, а другая – из прямого в острый к длинному основанию. Та диагональ, которая идёт к длинному основанию лежит напротив тупого угла трапеции, а значит она длиннее и короткого основания, и длинной боковой стороны (см. чертёж). Отсюда ясно, что указанная диагональ 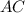 – может быть только диагональю идушей из прямого угла в тупой угол к короткому основанию. В соответствии с этим, расставим названия верщин трапеции
– может быть только диагональю идушей из прямого угла в тупой угол к короткому основанию. В соответствии с этим, расставим названия верщин трапеции 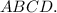 Значит,
Значит, 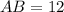 см, а
см, а 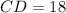 см.
см.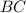 легко найти по теореме Пифагора:
легко найти по теореме Пифагора: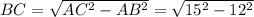 см =
см =  см
см 
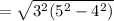 см
см 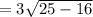 см
см 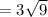 см
см 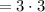 см
см 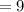 см ;
см ;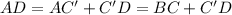 ;
;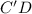 легко найти по теореме Пифагора, учитывая, что
легко найти по теореме Пифагора, учитывая, что 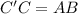 :
: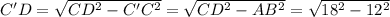 см
см 
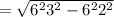 см
см 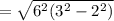 см
см 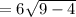 см
см 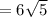 см ;
см ;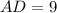 см
см 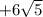 см ;
см ;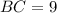 см ;
см ; 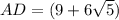 см .
см .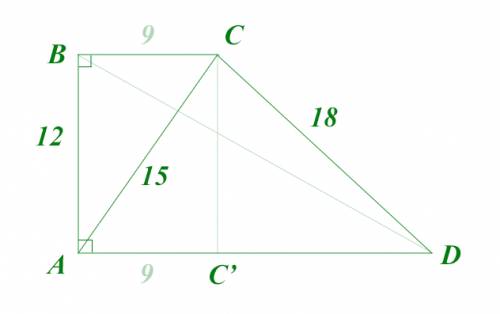
катеты xy=4
x=4/y
17=16/y2+y2
y4-17y2+16=0
y2=x
x2-17x+16=0
D=289-64=15^2
x1=1
x2=16
y1=1
y2=4
Числа 1 и 4, или 4 и 1