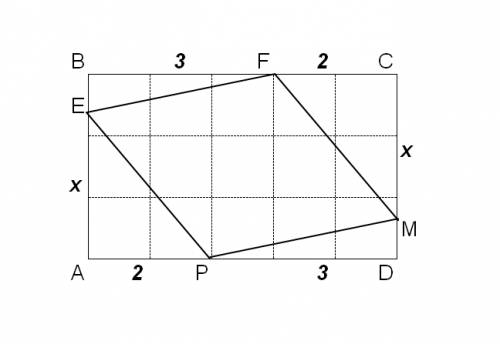
Из соображений симметрии FC=AP=2 и AE=CM=x (неизвестная длина)
Ромб - четырехугольник, у которого все стороны равны:
PE=EF=FM=MP (гипотенузы треугольников PAE, EBF, FCM, MDP)
По теореме Пифагора
2^2+x^2=(3-x)^2+3^2
4+x^2=9-6x+x^2+9
6x=14
x=7/3
Нашли все отрезки:
AE=CM=7/3
EB=MD=2/3
Далее находим сумму площадей всех треугольников PAE, EBF, FCM, MDP
St=(1/2)*2*(7/3)+(1/2)*3*(2/3)+(1/2)*2*(7/3)+(1/2)*3*(2/3)=7/3+1+7/3+1=20/3
Площадь прямоугольника S=5*3=15
Площадь ромба s=S-St=15-20/3=25/3
Отношение площадей прямоугольника и ромба
S/s=15/(25/3)=9/5
ответ: отношение площадей прямоугольника и ромба = 9/5
1)
Дана прямая призма ABCDA1B1C1D1.
ABCD-ромб (AB=BC=CD=AD=12). Угол BAD=60 гр, следовательно угол АВС=120.
Проведем прямые BD и B1D1, образующие квадрат.
Расмотрим треугольник ABD - равносторонний, т.к. угол ABD=60 гр (120/2 диагональ ромба является бисс-й). AB=BD=AD=12.
Vпр = S*h
Sосн = AD^2 * sin 60 = 144 * корень из / 2 = 72 корня из 3.
BB1D1D-квадрат. BD=DD1=12. DD1-высота призмы
V=12 * 72 корня из 3 = 864 корня из 3.
2)
Vпр=S*h
S=AD*BK=10*5=50
Рассмотрим треугольник B1BK-прямоугольный.
BB1^2 = B1K^2 - BK^2
BB1=12
V=12*50=600
Все углы при пересечении этих параллельных прямых секущей делятся на две группы:
тупые и острые.
Все тупые равны 123º
Все острые при этом являются смежными тупым углам, их сумма равна величине развернутого угла 180º. Они равны
180º-123º=57º
Какой угол чему равен - посмóтрите на данном к задаче рисунке.