ответ: a) 62°; б) 118°
Объяснение: Вопрос явно неполный - не указан второй из смежных углов. Правильно: Углы ABC и BCD – смежные, причем угол ABC равен 124 градуса. Найдите угол между перпендикуляром, проведенным из точки B к прямой AD и биссектрисой угла CBD.
* * *
Сумма смежных углов 180°, поэтому ∠СВD=180°- ∠ABC=180°-124°=56°.
Обозначим биссектрису угла СВD как ВМ. Биссектриса угла делит его пополам, поэтому ∠СВМ=∠DBM=56°:2=28°
У задачи 2 варианта решения.
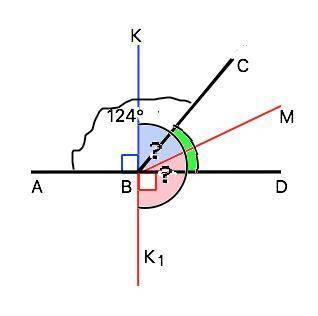
а) Перпендикуляр ВК к прямой AD лежит в той же полуплоскости, что луч ВС. Тогда искомый угол КВМ=∠КВD-∠MBD=90°-28°=62°
б) Перпендикуляр ВК1 лежит во второй полуплоскости. Тогда искомый угол К1ВМ=∠K1BD+∠DBM=90°+28°=118°
ответ: a) 62°; б) 118°
Объяснение: Вопрос явно неполный - не указан второй угол. Правильно: Углы ABC и BCD – смежные, причем угол ABC равен 124 градуса. Найдите угол между перпендикуляром, проведенным из точки B к прямой AD и биссектрисой угла CBD.
* * *
Сумма смежных углов 180°, поэтому ∠СВD=180°- ∠ABC=180°-124°=56°.
Обозначим биссектрису угла СВD как ВМ. Биссектриса угла делит его пополам, поэтому ∠СВМ=∠DBM=56°:2=28°
У задачи 2 варианта решения.
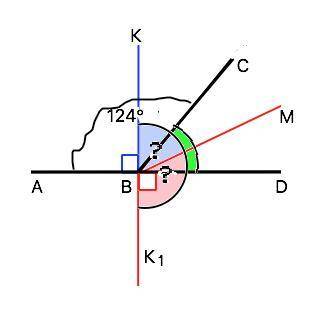
а) Перпендикуляр ВК к прямой AD лежит в той же полуплоскости, что луч ВС. Тогда искомый угол КВМ=∠КВD-∠MBD=90°-28°=62°
б) Перпендикуляр ВК1 лежит во второй полуплоскости. Тогда искомый угол К1ВМ=∠K1BD+∠DBM=90°+28°=118°
Назовем трапецию АВСD, а точка пересечения прямых, содержащих боковые стоторы - О, высота - ВН.
S трапеции = (AD+BC)/2 *BH=12. Так как ВН=2 то получим AD+ВС=12.
Трапеция равнобокая, значит угол ВАН равен углу CDA (углы при основании).
Треугольник АОD прямоугольный (угол AOD прямой), а так как углы ВАН и СDА равны, то этот треугольник еще и равнобедренный. В нем один угол прямой, а значит два других (ВАН и СDА) по 45 градусов.
Опустим из вершины С высоту СМ. Треугольники ВАН и СDМ равны между собой (угол ВАН= углуСDА, АВ=СD).
В треугольнике ВАН угол ВНА=90 градусов, угол ВАН=45 градусов, значит треугольник равнобедренный. Из этого следует что ВН=АН=2.
Так как треугольники ВАН и СDА равны, то DМ=2.
AD= АН+НМ+ МD, BC+AD=12, BC=HM (как сторны прямоугольника),
4+2ВС=12, 2ВС=8, ВС=4, а значит AD=8.
Треугольник ВАН прямоугольный, значит АВ= корень квадратный из (АН^2+BH^2)= корень квадратный из (8) или 2*(корень квадратный из 2).
ОТВЕТ: 4, 8, 2*(корень квадратный из 2).