Дано:
a=7см
b=24см
Найти:
Sin, Cos, tg острого угла - ?
с=√7²+24²=√49+576=√625=25 см
против большей стороны лежит больший угол, и наоборот, против меньшей - меньший угол B < углу A ⇒ ищем Sin, Cos, tg острого угола А (см рисунок)
Синус - это отношение противолежащего катета к гипотенузе ⇒ SinA=BC/AB=24/25
Косинус - это отношение прилежащего катета к гипотенузе ⇒ CosA=AC/AB=7/25
Тангенс - это отношение противолежащего катета к прилежащему или отношение синуса к косинусу ⇒ tgA=BC/AC=24/7 или tgA=SinA/CosA=(24/25)/(7/25)=24/7
ответ: Sin большего острого угла равен 24/25, Cos большего острого угла равен 7/25, tg большего острого угла равен 24/7
Дано:
a=7см
b=24см
Найти:
Sin, Cos, tg острого угла - ?
с=√7²+24²=√49+576=√625=25 см
против большей стороны лежит больший угол, и наоборот, против меньшей - меньший угол B < углу A ⇒ ищем Sin, Cos, tg острого угола А (см рисунок)
Синус - это отношение противолежащего катета к гипотенузе ⇒ SinA=BC/AB=24/25
Косинус - это отношение прилежащего катета к гипотенузе ⇒ CosA=AC/AB=7/25
Тангенс - это отношение противолежащего катета к прилежащему или отношение синуса к косинусу ⇒ tgA=BC/AC=24/7 или tgA=SinA/CosA=(24/25)/(7/25)=24/7
ответ: Sin большего острого угла равен 24/25, Cos большего острого угла равен 7/25, tg большего острого угла равен 24/7
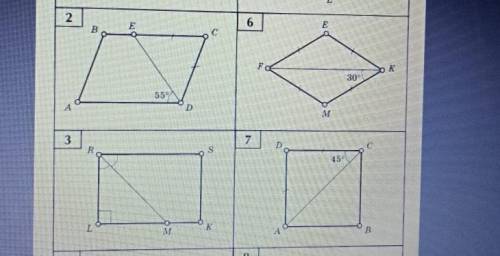
1. В параллелограмме противоположные стороны параллельны, то есть BC||AD, AB||CD, тогда мы можем воспользоваться теоремами о равенстве углов в параллельных прямых (BC и AD) с секущей ED: угол EDA = углу DEC=55°, как накрест лежащие углы в параллельных прямых;
2. Рассмотрим треугольник ECD, по условию он равнобедренный, так как EC = CD, а следовательно углы при основании этого треугольника равны, то есть DEC = CDE = 55°;
3. Сумма углов треугольника равна 180°, значит угол С = 180° - (DCE + CDE) = 180-110 = 70°, так как ABCD - параллелограмм, то противоположные углы равны: угол B = углу D, угол С = углу А = 70°;
4. Так как противоположные углы равны, можем найти угол В = углу D:
Угол D = угол ADE + угол CDE = 110°, следовательно угол D = углу B = 110°;
ответ: угол D = углу B = 110°, угол А = углу С = 70°.
•Номер 3
1. В прямоугольнике LRSK все углы прямые, то есть равны 90°;
2. Угол LRM = углу MRS = угол R/2 = 90/2 = 45°;
3. В прямоугольнике противоположные стороны параллельны, тогда угол RMK = 180 - угол MRS, как односторонний с углом MRS в параллельных прямых с секущей RM = 180 - 45° = 135°;
4. В прямоугольном треугольнике RLM угол RML = 90 - угол LRM = 45°;
ответ: угол LRM = углу MRS = 45°, угол RML = 45°, угол RMK = 135°.
•Номер 6
1. В ромбе FEKM все стороны равны;
2. Рассмотрим равнобедренный треугольник FMK (так как FM = MK), в нем углы при основании равны, значит угол FKM = углу KFM = 30°;
3. Сумма углов треугольника равна 180°, тогда угол M = 180° - (FKM + KFM) = 180-60 = 120°;
4. В ромбе противоположные углы равны, тогда угол М = углу Е = 120°;
5. Диагональ FK ромба имеет свойство делить углы фигуры пополам, значит угол F = углу K = 2•MFK = 60°;
ответ: угол F = K = 60°, угол M = E = 120°;
•Номер 7
1. ABCD - квадрат, так как AD = DC;
2. Диагональ AC квадрат делит его углы пополам, так как в квадрате все углы равны 90° (угол А = углу В = углу С = углу D = 90°), значит угол DCA = DAC = CAB = ACB = 45°;
ответ: DCA = DAC = CAB = ACB = 45°.