Впрямоугольном треугольнике катет, прилегающий к углу 30 градусов равен 18 см. найдите длину биссектрисы этого треугольника, проведенную к этому катету. нужно!

👇

Увидеть ответ

Ответ:

STRELOK9999

19.05.2023

обозначим известный катет за а, а=18, угол А =30 градусам, угол С=90 градусам.

один угол прямоугольного треугольника равен 30 градусам, значит 2 угол равен 60 градусам.

Воспользуемся теоремой синусов и углом в 60 грудусов для нахождения гипотенузы(обозначим ее за с):

$\frac{18}{c}=\frac{\sqrt{3}}{2}$ $c=12\sqrt{3}$

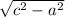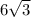
находим второй катет (б) = $\sqrt{c^2-a^2}$ = $6\sqrt{3}$

т.к. из угла в 60 градусов проводят биссектрису, каждый из образовавшихся углов равен 30 градусам. рассмотрим треугольник образовавшийся стороной б и бессектрисой к стороне а.

для нахождения гиппотенузы(искомый компоннт, обозначим за к) воспользуемся теоремой косинуса:

$\frac{6 \sqrt{3} }{k}=\frac{\sqrt{3}}{2}$

k=12

4,4(2 оценок)

Открыть все ответы

Ответ:

Лубаша

19.05.2023

Опустим из вершины В высоту ВE на основание AD.

Из вершины С высоту CF. Нижнее основание делится на три отрезка, причем АЕ=FD, а EF=ВС, обозначим AE и FD как х, а EF и BC, как у.

ТОгда средняя линия равна KL=(BC+AD)/2=(x+2y+x)/2=x+y

Т.е. нам нужно найти длину отрезка ED, который равен x+y

Рассмотрим треугольник EBD, он прямоугольный и его угол BDE=60, тогда угол EBD=90-60=30.

Как мы знаем, что катет противолежалий углу 30 градусов равен половине гиппотенузе. Гиппотенуза у нас BD=4, тогда ED=KL=2

ответ: KL=2

4,6(16 оценок)

Ответ:

skladnova03

19.05.2023

Теорема:
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Доказательство:
Рассмотрим треугольники АВС и А1В1С1, у которых АВ=А1В1, угол А= углу А1, угол В=углу В1. Докажем, что треугольник АВС=треугольнику А1В1С1.
Наложим треугольник АВС на треугольник А1В1С1, так, чтобы вершина А совместилась с вершиноу А1, сторона АВ совместилась с равной ей стороной А1В1, а вершины С и С1 оказались по одну сторону от прямой А1В1.
Так как угол А= углу А1 и угол В=углу В1, то сторона АС наложится на луч А1С1, а сторона ВС- на луч В1С1. Поэтому вершина С - общая точка сторон АС и ВС - окажется лежащей как на луче А1С1, так и на луче В1С1 и, следовательно, совместятся с общей точкой этих лучей - вершиной С. Значит совместятся стороны АС и А1С1, АС и В1С1.
Итак, треугольник АВС и А1В1С1 полностью совместятся, поэтому они равны. Теорема доказана.

4,7(71 оценок)

Это интересно:

Взаимоотношения

12.10.2021

Как разорвать старые отношения, если у вас уже появился новый парень...

Хобби-и-рукоделие

07.03.2023

Как играть в Колонизаторов...

Кулинария-и-гостеприимство

04.02.2023

Как приготовить фасоль пинто: пошаговый рецепт и полезные советы...

Образование-и-коммуникации