
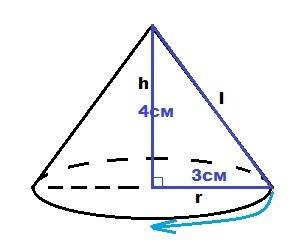
При вращении прямоугольного треугольника вокруг большего катета образуется конус, у которого высотой является больший катет, а радиусом основания будет меньший катет. Образующей конуса является гипотенуза треугольника.
h = 4 см; r = 3 см
Образующая по теореме Пифагора из прямоугольного треугольника
l² = h² + r² = 4² + 3² = 25
l = 5 см
Основание конуса - круг с площадью
S₀ = πr² = π*3²; S₀ = 9π см²
Площадь боковой поверхности конуса
S₆ = πrl = π*3*5; S₆ = 15π см²
Площадь полной поверхности конуса
S = S₀ + S₆ = 9π + 15π = 24π см²
ответ: площадь полной поверхности конуса 24π см²
Объяснение:
вы должны рассматривать высоту как катет прямоугольного треунольника. сначала начертите призму . проведите диагональное сечение . потом проведя диагональ самой призмы вы увидите что сечение разбивается на два прямоугольных треугольника .
ABCDA1B1C1D1 призма
BDB1D1 диагональное сечение
BD1 диагональ призмы.
по правилам прямоугольного треугольника если угол=30' то противоположный катет равен половине гипотенузы
по условию задачи гипотенуза это диагональ BD1
а катет равный половине гипотенузы это диагональ основания BD
в основание квадрат =>BD= 4V2 (V корень кв.)
BD1= 2*4V2=8V2
по теореме Пифагора DD1^2=(8V2)^2-(4V2)^2= 96
DD1=4V6
надеюсь правильно