
90°.
Объяснение:
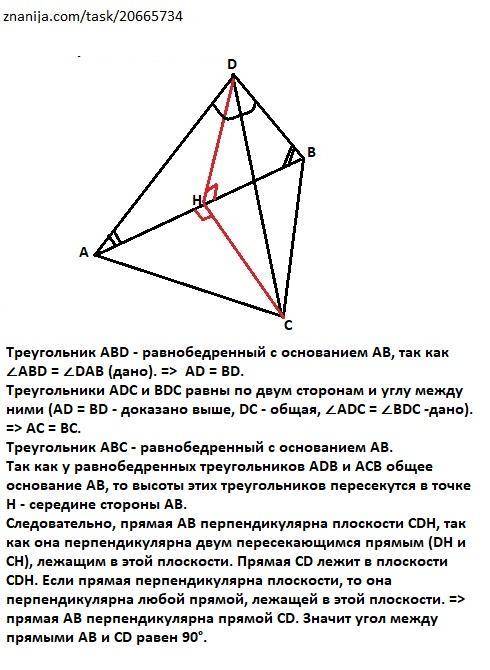
Треугольник ABD - равнобедренный с основанием АВ, так как ∠ABD = ∠DAB (дано). => AD = BD.
Треугольники ADC и BDC равны по двум сторонам и углу между ними (AD = BD - доказано выше, DС - общая, ∠ADС = ∠BDC -дано). => AC = ВС.
Треугольник АВС - равнобедренный с основанием АВ.
Так как у равнобедренных треугольников ADB и ACB общее основание АВ, то высоты этих треугольников пересекутся в точке Н - середине стороны АВ.
Следовательно, прямая АВ перпендикулярна плоскости CDH, так как она перпендикулярна двум пересекающимся прямым (DH и CH), лежащим в этой плоскости. Прямая CD лежит в плоскости CDH. Если прямая перпендикулярна плоскости, то она перпендикулярна любой прямой, лежащей в этой плоскости. => прямая АВ перпендикулярна прямой CD. Значит угол между прямыми АВ и CD равен 90°.
Объяснение:
Нужны:
1. Сумма углов треугольника
2.Теорема синусов.
Треугольник имеет шесть основных элементов: три угла A, B, C и три стороны a, b, c.
Решить треугольник – значит найти все эти шесть элементов.
Известны 2 угла и 1 сторона. Найти третий угол и две стороны.
Третий угол С =180-48-64=68°
ва с 14
= = = =15.1
sin(48°) sin(64°) sin(68°)0.9272
(точки - между а,в, с -для выдержки расстояния, иначе дробь не получается)
в= 0.7431*15.1= 11.22см
а=0.8988*15.1= 13.6см
Проверка:
с²=а²+ в²-2ав*cos(68°)
с²=184.96+ 125.89 -305.184(0.3746=184.96+125.89=114.32=196
с²=196
с=14