Question

И КАК МОЖНО ПОДРОБНЕЕ найти углы равнобедренной трапеции если один из углов на 45 градусов больше другого​

Answer 1

4х+90°=360°

х=67,5 - 2 угла которые меньше 90°(острые) (х)

67,5+45=112,5° - 2 угла которые больше 90°(тупые) (х+45)

Объяснение:

Пусть х=k х - например ∠А и ∠В, а х+45 - ∠С и ∠D

k-коефициент

Answer 2

<A=67,5°

<D=67,5

<B=112,5°

<C=112,5°

Объяснение:

Дано

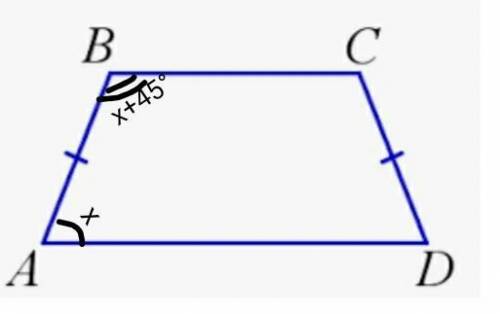
АВСD- равнобокая трапеция

АВ=CD

<A=?

<B=? на 45°больше >А

Найти <А; <В; <С;<D

Сумма углов прилежащих к боковой стороне трапеции равна 180°.

<А+<В=180°.

Пусть градусная мера угла <А будет х°, тогда градусная мера угла <В будет (х+45°).

Составляем уравнение

х+х+45=180

2х=180-45

2х=135

х=135/2

х=67,5° градусная мера угла <А

Градусная мера угла <В (х+45), подставляем значение х

67,5+45=112,5°

По свойствам равнобокой трапеции

<А=<D;

<B=<C