16.
а)
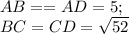
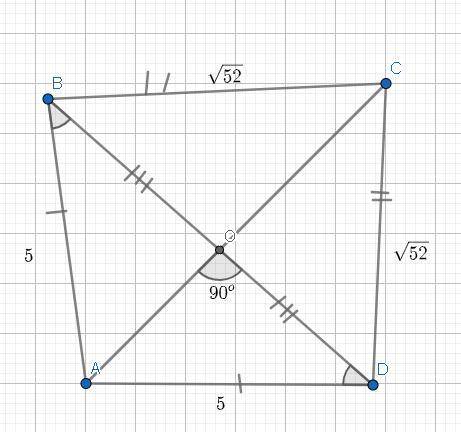
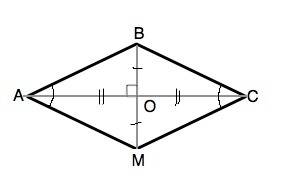
Диагональ BD — делит четырёхугольник на 2 произвольных треугольника: ΔBCD; ΔBAD.
Проведём также диагональ CA: он проходит через ΔBCD.
ΔBCD — равнобёдренный, так как: 
А в свойствах равнобёдренного треугольника входит то, что высота, медиана, и биссектриса, проведённая с вершины к основанию — одно и то же, что и означает, что наш отрезок CO — медиана, и поэтому делит диагональ BD — на 2 равные части.
б)
Я не вижу в этом варианте заданное условие. А если она и вправду есть, то найти площадь, зная то, что отрезки являются "целыми числами", я не смогу.
Но площадь четырёхугольника можно найти — зная всего-лишь его стороны: 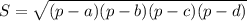
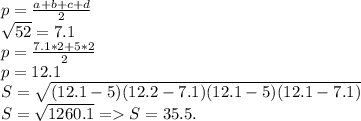
В параллелограмме противоположные углы равны, противоположные стороны равны и параллельны, а диагонали точкой пересечения делятся пополам.
а)
В параллелограмме АВСD диагонали взаимно перпендикулярны. Следовательно, катеты четырех прямоугольных треугольников, образованных диагоналями и сторонами ромба, равны. =>
Эти четыре треугольника равны, значит, их гипотенузы ( стороны параллелограмма) - равны. АВСD- ромб.
б)
Если диагональ параллелограмма - биссектриса его угла, то по свойству равенства накрестлежащих углов при параллельных прямых и секущей она она делит и противоположный угол пополам и является основанием треугольника с равными углами. Равенство углов при основании - признак равнобедренного треугольника.
Поэтому АВ =ВС, ВС =СD, АD =АВ.
Параллелограмм АВСD - ромб.
ответ: DJ r SF gthuhthh
Объяснение:will CEO vs WWII on x wry k MB