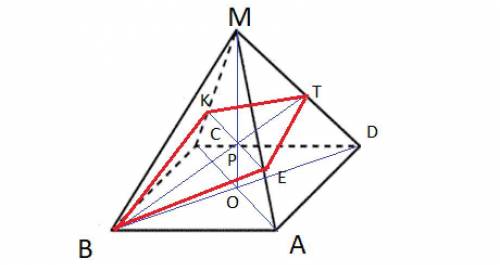
В сечении пирамиды плоскостью, проходящей через точку В и середину ребра MD параллельно прямой AC, образуется четырёхугольник, состоящий из двух равнобедренных треугольников.
Большая диагональ его - это медиана ВТ треугольника BMD.
Боковые стороны по 18, BD = 9√2 как диагональ квадрата.
Используем формулу медианы:
ВТ = (1/2)√(2*(9√2)² + 2*18² - 18²) = (1/2)√648 = 9√2.
Так как высота МО пирамиды - тоже медиана, то ВТ делится точкой Р 2:1.
Отрезок ЕК = (2/3)АС = (2/3)*9√2 = 6√2.
ВР = (2/3)ВТ = (2/3)*9√2 = 6√2, РТ = 3√2.
ответ: S = (1/2)*(6√2*6√2 + 3√2*6√2) = (72 + 36)/2 = 54 кв.ед.
Все рёбра треугольной пирамиды равны. Найти угол наклона:
а) Бокового ребра к плоскости основы.
б) боковой грани к площине основы/
Объяснение:
АВСМ -пирамида, пусть ребро равно х.
a)Угол наклона бокового ребра к плоскости основания это ∠МАО.
Т.к АВ=ВС=АС, то высота проецируется в центр основания О , точку пересечения медиан.Тогда АО=2/3*АН, где АН медиана, ВН=х/2 .
Из ΔАВН-прямоугольного, АН=√(х²-х²/4)=(х√3)/2. Тогда АО=( х√3)/3.
ΔАОМ-прямоугольный, cos∠МАО=АО/АМ , cos∠МАО=( х√3)/3:х=√3/3,
∠МАО=arccos(√3/3) .
ОМ=√(х²-( х√3)/3)² )=(х√6)/3
б)В равностороннем ΔАВС , медиана АН является высотой . Тогда МН⊥ВС по т. о трех перпендикулярах и ∠АНМ-линейный угол между боковой гранью и плоскостью основания.
ОН=1/3*АН , ОН=(х√3)/6.
ΔОНМ-прямоугольный ,tg∠AHM=MO/OH , tg∠AHM=2√2 , ∠AHM=arctg(2√2).