Question

Найдите площадь треугольника ABC, изображённого на рисунке ​

Answer 1

3

Объяснение:

SΔ=1/2*a*h  (половина основания на высоту)

Найдём площадь этого треугольника(ABC), с вычитания меньшей площади из большей.

BH=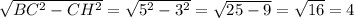$\sqrt{BC^2-CH^2} = \sqrt{5^2-3^2} =\sqrt{25-9} =\sqrt{16} = 4$

AH=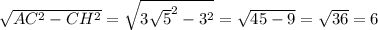$\sqrt{AC^2-CH^2} = \sqrt{3\sqrt{5} ^2-3^2} =\sqrt{45-9} =\sqrt{36} = 6$

SΔBCH=1/2*a*h =1/2*4*3=6

SΔACH=1/2*a*h =1/2*6*3=9

SΔACB=SΔACH-SΔBCH= 9 - 6 =3