С линейки начертим остроугольный треугольник ABC, при этом AB < BC.В этом треугольнике есть высота H, как и в других.Теперь проведём ровную линию от точки B до H.Так же сказано, чтобы провести линию от медианы M до B.На рисунке показано где расположена медиана M.(M середина AC)
2.Сначала изобразим обычный отрезок a.Так же изобразим c, при этом c>a.
Нарисуем прямоугольный треугольник ABC.
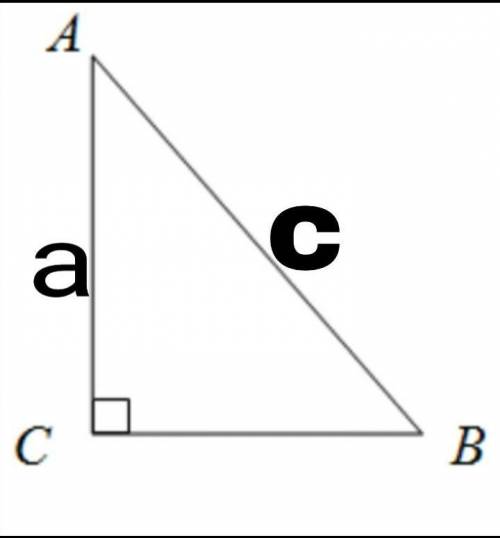
В задании сказано изобразить прямоуг. треуг. с катетом а и гипотинузой с.В таком треугольнике 2 катета и 1 гипотинуза.Катет a расположен между A и C.Разумеется длина катета равна длине отрезка а.
Гипотенуза с находится между A и B.
Разумеется длина гипотенузы равна длине отрезка с
ответ:всё на рисунках.
P.S. на 2 рис. я выделил a и c это отрезки которые вошли в треуг.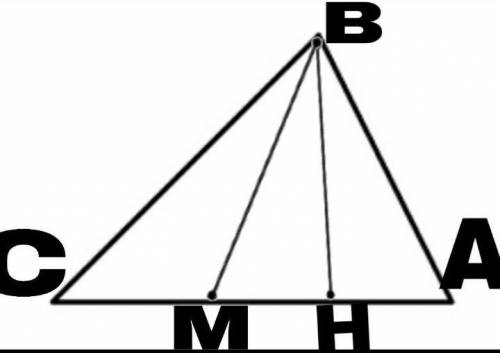
Объяснение:
Сначала найдем стороны параллелограмма
( 5 + 6 ) * 2 = 22 части приходится на все четыре стороны параллелограмма
44 \ 22 = 2 см - приходится на одну часть
2 * 5 = 10 см - ширина параллелограмма
2 * 6 = 12 см - длина параллелограмма
cos A = АН \ АВ = АН : 10
Составляем пропорцию и решаем ее
3 : 5
АН : 10
АН = 3 * 10 \ 5 = 6 см
По теореме Пифагора находим высоту - ВН
ВН = √АВ² - АН² = √100 - 36 =√64 = 8 см
Для нахождения площади трапеции нам нужно знать длину обоих оснований
НD = 12 - 6 = 6 см длина нижнего основания трапеции
( ВС + НD) \ 2 * ВН = ( 12 + 6 ) \ 2 * 8 = 72 см² - площадь трапеции НВСD
Объяснение:
2.
Строим отрезки а и с
Произвольно ставим точку, обозначим ее как точку А,
Циркулем чертим окружность с центром в точке A и радиусом равным отрезку a (на рисунке красного цвета)
Произвольно выбираем на построенной окружности точку, обозначим ее как точку B
Циркулем чертим окружность с центром в точке A, и радиусом равным отрезку c (на рисунке синего цвета)
По линейке строим перпендикуляр к прямой AB,
В точке пересечения перпендикуляра с синей окружностью, ставим точку C, соединяем точки С и А, получая требуемый треугольник.
1.
Строим произвольный треугольник ABC, у которого все углы острые.
Циркулем чертим окружность с центром в точке C и произвольным радиусом, больше чем сторона АС (на рисунке зеленого цвета)
Тем же радиусом чертим окружность с центром в точке A и (на рисунке коричневого цвета)
Получаем две точки К и N, в местах пересечения окружностей.
Соединяем К и N, получая точку М, являющуюся серединой стороны AC.
Высота из точки B строится по линейке, как перпендикуляр к стороне AC