пусть треугольник abc :
ab =18 см ;
вписанный прямоугольник mnef ( m∈[ac] , n∈ [bc] , e , f ∈ [ ab] ) .
a) mf : mn = 2 : 5 . mf =2x ; mn =5x ; p =2(mf+mn) =2(2x+5x) =14x.
в δafm : af =mf =2x ;
в δben : be =ne =mf =2x ;
af +fe +eb =18 см ; * * *fe=mn =5x * * *
2x +5x+2x =18⇒ x =2(см)
p =14x =14*2 см =28 см.
б) mf : mn = 5 : 2. mf =5x ; mn =2x ; p =2(mf+mn) =2(5x+2x) =14x.
5x +2x+5x =18⇒12x =18⇔x=1,5 (см) .
p =14x=14*1,5 см = 21 см .
ответ : 28 см , 21 см .
периметр ромба равен 4а.
решение.
меньшая диагональ ромба равна а. это как раз диагональ проведенная из вершины тупого угла и образует с высотой угол 30 град. высота - это перпендикуляр к противоположно стороне ромба (т.е.) образует угол 90 град. т.к. сумма углов треугольника равна 180, то угол между короткой диагональю и стороной ромба равен 60 град. получается, что короткая диагональ делит ромб на 2 равносторонних треугольника и диагональ равна стороне ромба, т.е. а. таким образом периметр равен 4а
Объяснение:
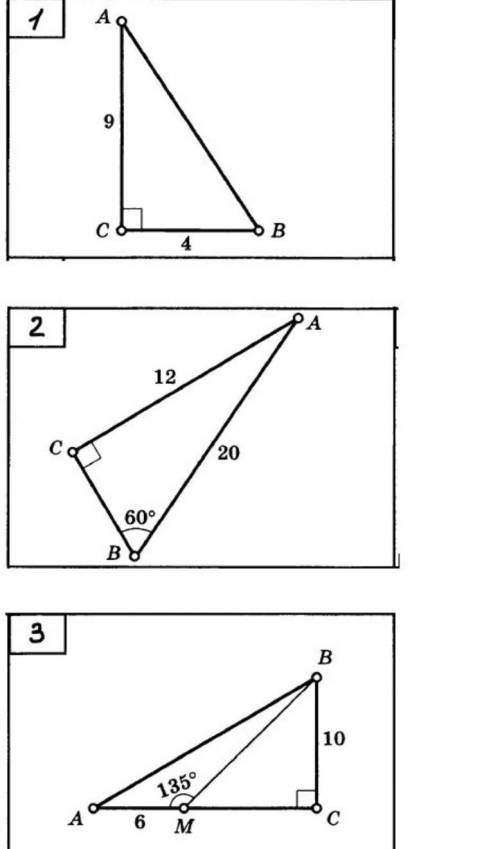
1)
Площадь прямоугольного треугольника равна половине произведения двух катетов.
SABC=AC*CB/2==9*4/2=18см².
ответ: 18см²
2)
∆АВС- прямоугольный.
СВ и АС- катеты
АВ- гипотенуза.
По теореме Пифагора найдем катет
СВ²=СВ²-СА²=20²-12²=400-144=256
СВ=√256=16 см.
SABC=AC*CB/2=12*16/2=96 см²
ответ:96см²
3)
<АМС=180°, развернутый угол.
<ВМС=<АМС-<АМВ=180°-135°=45°
∆МСВ - прямоугольный, равнобедренный
<СМВ=<МВС=45°
ВС=МС
МС=10см.
АС=АМ+МС=6+10=16см.
SABC=16*10/2=80cм²
ответ:80см²