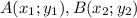
Координаты середины отрезка
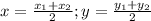
Расстояние между точками
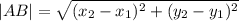
А(-4;-4), B(-4;2), C(4;2), D(8;-4)
MN - средняя линия трапеции.
M - середина AB
M( (-4+(-4))/2 ; (-4+2)/2 ) = M(-4;-1)
N - середина CD
N( (4+8)/2 ; (2+(-4))/2 ) = N(6;-1)
|MN|= √( (6-(-4))^2 + (-1-(-1))^2 ) =√(100+0) =10
Точки A и D имеют равные координаты по оси Y => AD||X'X (отрезок AD параллелен оси X)
Аналогично BC.
Основания параллельны оси X.
Точки A и B имеют равные координаты по оси X => AB⊥X'X (отрезок AB перпендикулярен оси X)
AB - высота трапеции.
|AB|= √( (-4-(-4))^2 + (2-(-4))^2 ) =√(0+36) =6
S(ABCD) =MN*AB =10*6 =60
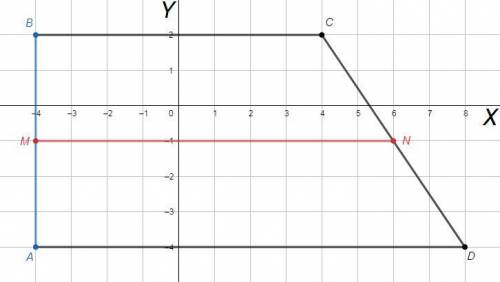
если x не равно 0, то разделив левую и правую части уравнения на x, получим
m =((5-y)/x) n, где ((5-y)/x) какое-то число.
По условию коллинеарности:Два вектора a и b коллинеарны, если существует число не равное нулю n такое, что a = n · b
Следовательно, если a и b не коллинеарны то такого числа не существует.
А в нашем примере такое число есть (при x не равном 0).
Следовательно если x не равно 0, то векторы коллинеарны.
А так как по условию они не коллинеарны, то x = 0. Тогда и y = 0.
ответ: x = 0 и y = 0