Примем ребро куба за 1.
Ребро АА1 параллельно заданному ребру ВВ1, кроме того, оно пересекает заданную плоскость.
Поэтому заданный угол можно искать между прямой АА1 и плоскостью (AMF).
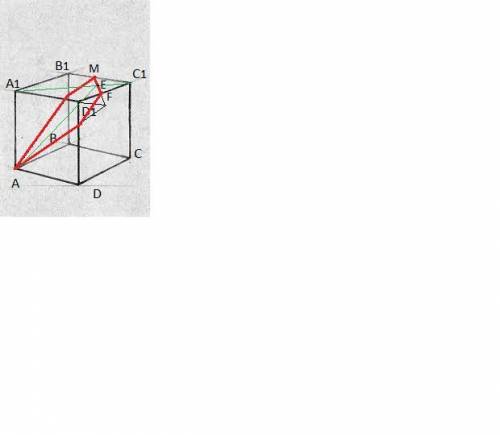
Если проведём диагональное сечение куба, то получим искомый угол АА1Е, где Е - точка пересечения диагонали верхней грани и отрезка MF. Точка Е - это середина MF.
В прямоугольном треугольнике С1MF отрезок С1Е равен 0,5*cos 45° = 0,5/√2 = √2/4.
Наш искомый угол - это угол А1АЕ.
Находим катет АА1Е = А1С1 - С1Е = √2 - (√2/4) = 3√2/4.
ответ: угол между прямой BB1 и плоскостью (AMF) равен углу между прямой AA1 и А1Е и равен arc tg((3√2/4)/1) = arc tg(3√2/4).
В угловой мере это 0,814827 радиан или 46,686143 градуса.
Трапеция АВСД, АВ=СД. уголА=уголД, уголВ=уголС, точка касания М на АВ, точка К на ВС, точка Р на СД, точка Т на АД, ДР=8, ДТ=ДР=8 как касательные проведенные из одной точки, АТ=АМ=8 как касательные проведенные из одной точки и потому что уголА=уголД, МВ=ВК=х как касательные проведенные из одной точки, СК=СР=х как касательные проведенные из одной точки (уголВ=уголС), периметр=8+8+8+8+х+х+х+х, 60=32+4х, х=7, ВС=7+7=14, АВ=8+7=15=СД, АД=8+8=16
Объяснение: