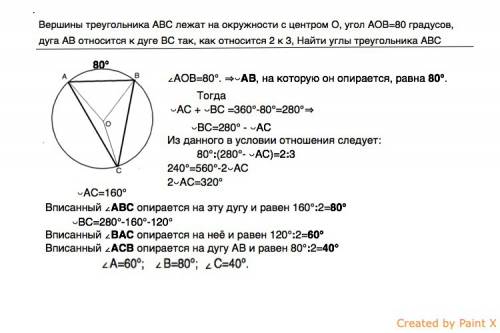
При измерениях 4-угольной правильной пирамиды получили следующие средние значения прямых измерений и их абсолютные погрешности Сторона основания l = 1,07 см, ∆l=0,03 см
Высота h = 2,99 см , ∆h=0,12 см
Рассчитать средний объем пирамиды, зная, что V=1/3 S_осн h.
Вывести формулу для расчета ∆V ̅
Результат представить в виде V=V ̅±∆V ̅, см3.
Чему равна относительная погрешность?
Чертеж, я думаю, сумеешь сам нарисовать. Ромб с вершинами А,В,С,D
Черти диагонали. Они пересекаются под прямым углом и в точке пересечения делятся пополам(как ромбу и полагается). Диагонали АС и BD. Точка пересечения диагоналей О.
Дано: АВ=50 см, т.к все стороны ромба равны, т.е. 200/4=50
Получились 4 прямоугольных треугольника, равных друг другу. S ромба = 4*S abo
S abo=1/2AO*BO (площадь прямоугольного треугольника равна половине произведения катетов)
Диагонами ромба относятся друг к другу как 3:4
Катеты треугольника АВО обозначаем как 3х и 4х (т.к. половины диагоналей тоже соотносятся друг с другом как 3:4)
Т.О. получается прямоугольный треугольник с катетами 3х и 4х, и с гипотенузой 50 см.
Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов.
Гипотенуза = 50 см.
Получаем:
АВ=1/2АО*ВО
2500=(3х)2+(4х)2
2-это в квадрате
2500=9х2+16х2
2500=25х2
х2=100
х=10
S abo=1/2AO*BO
AO=3x=30 см
BO=4x=40 см
S abo=1/2*30*40=600
S abcd=4*600=2400
ответ: площадь ромба = 2400 см2