1)
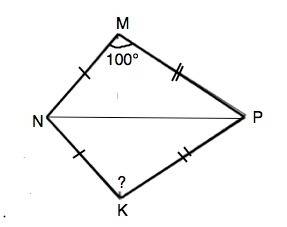
Проведем диагональ NP. Треугольники PMN и PKN равны по трем сторонам - две по условию, третья - общая. .
Следовательно, углы при вершинах К и М равны. Угол К=100°
2)
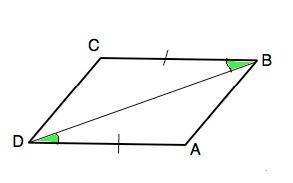
Диагональ BD делит четырехугольник на треугольники ∆ ABD и ∆ CBD. В этих треугольниках стороны ВС=АD по условию, DB общая, углы между этими сторонами равны. ∆ ABD и ∆ CBD равны по первому признаку равенства треугольников.
Следовательно, стороны АВ=CD.
Если противоположные стороны четырехугольника равны, этот четырехугольник - параллелограмм. ⇒, АВ||CD. Доказано.
Задача на подобие треугольников.
АВ и СД перпендикулярны плоскости α и поэтому параллельны между собой.
Два прямоугольных треугольника PCD и АВР подобны по равенству углов. (Если в прямоугольных треугольниках равен один из острых углов, то они подобны)
Из подобия треугольников вытекает отношение
АВ:СD=PB:PD
Пусть PD=x, тогда РВ= BD+PD=3+x
12:3=(x+3):x
Произведение крайних членов пропорции равно произведению ее средних членов.
12х=3х+9
9х=9
х=1
PD=1 см