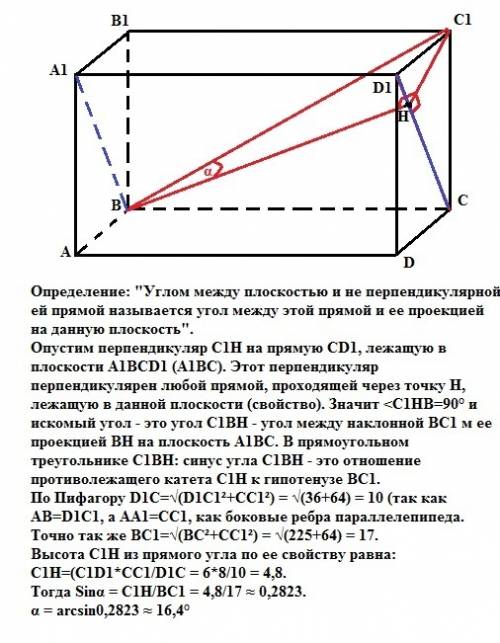
Определение: "Углом между плоскостью и не перпендикулярной ей прямой называется угол между этой прямой и ее проекцией на данную плоскость".
Опустим перпендикуляр С1Н на прямую СD1, лежащую в плоскости А1ВС (это плоскость А1ВСD1, так как секущая плоскость пересекает параллельные плоскости АА1В1В и DD1C1C по параллельным прямым А1В и D1C). Отрезок С1Н перпендикулярен любой прямой, проходящей через точку Н, лежащую в данной плоскости (свойство). Значит <C1HB=90° и искомый угол - это угол С1ВН - угол между наклонной ВС1 м ее проекцией ВН на плоскость А1ВС. В прямоугольном треугольнике С1ВН: синус угла С1ВН - это отношение противолежащего катета С1Н к гипотенузе ВС1.
По Пифагору D1C=√(D1C1²+CC1²) = √(36+64) = 10 ед (так как АВ=D1C1, a AA1=CC1, как боковые ребра параллелепипеда.
Точно так же ВС1=√(ВC²+CC1²) = √(225+64) = 17 ед.
Высота С1Н из прямого угла по ее свойству равна:
С1Н=(С1D1*CC1/D1C = 6*8/10 = 4,8 ед.
Тогда Sinα = C1H/BC1 = 4,8/17 ≈ 0,2823.
α = arcsin0,2823 ≈ 16,4°.
1)Геометрическое преобразование плоскости — взаимно-однозначное отображение этой плоскости на себя. Наиболее важными геометрическими преобразованиями являются движения, т. е. преобразования, сохраняющие расстояние.
2)
Преобразование плоскости (или пространства), при котором сохраняется отношение расстояний, называется преобразованием подобия или просто подобием. Другими словами, при преобразовании подобия F для любых двух точек имеет место соотношение F(A)F(B) = kAB, где k – некоторое число, называемое коэффициентом подобия.
3)
Две фигуры называют гомотетичными, если одна из них переходит в другую при некоторой гомотетии. Из определения следует, что при $k=-1$ гомотетия является центральной симметрией с центром в точке $O$, а при $k=1$ — тождественным преобразованием
4)Гомоте́тия (от др.-греч. ὁμός «одинаковый» + θετος «расположенный») — преобразование плоскости (или пространства), заданное центром O и коэффициентом {\displaystyle k\neq 0}k\neq 0, переводящее каждую точку {\displaystyle X}X в точку {\displaystyle X'}X' такую, что {\displaystyle {\overrightarrow {OX'}}=k{\overrightarrow {OX}}}\overrightarrow {OX'}=k\overrightarrow {OX}. При этом центр остаётся на месте. Гомотетию с центром O и коэффициентом k часто обозначают через Н^k O