
Объяснение:
Отношение сторон данного треугольника 6:8:10=3:4:5 соответствует египетскому, т.е. прямоугольному.
а)
Биссектриса треугольника делит противоположную сторону на отрезки, соответственно пропорциональны двум другим сторонам. =>
СD:DА=ВС:ВА
СD:DА=6:10=3:5
АС=3+5=8 частей.
1 часть=8:8=1
СD=3•1=3
Из прямоугольного ∆ СВD по т.Пифагора ВD=√(ВС^2+СD^2)=√(36+9)=3√5
б)
Для биссектрисы острого угла прямоугольного треугольника есть формула
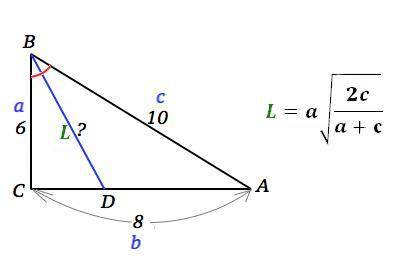
L=a•√(2c:(a+c)), где L- биссектриса, а и с -соответственно катет, прилежащий углу, и гипотенуза.
L=6•√(2•10:(6+10))=6√(5:4)=3√5
Проведем диагонали: AC и BD, они пересекаются в точке O, под углом 90 градусов. Наш ромб разделился на 4 равных треугольника (по свойству диагоналей в ромбе). Рассмотрим один из них, например: ABO. Угол AOB равен 90 градусам, а угол ABO возьмем за 40 градусов. Сумма углов треугольнике равна 180 градусам, проводим следующее действие: 180-(90+40)=50 градусов, мы нашли угол OAB. Вернемся к ромбу, т.к. угол OAB равен 50 градусам, угол BAD, в ромбе, равен 100 градусам. Диагональ BD делит ромб на 2 равных треугольника: BAD и BCD (значит, углы BAD и BCD равны). Сумма углов в 4-угольнике равна 360 градусам, проведем следующее действие: 360-100*2=160 градусов (осталось на углы ABC и ADC) . Углы OBA и DOE равны, как соответственные (оба по 40 градусов), проведем следующее действие: (160-40*2)/2=40 (углы BOC и AOD, опять же, как соответственные).