остроугольный и равнобедренный.
Объяснение:
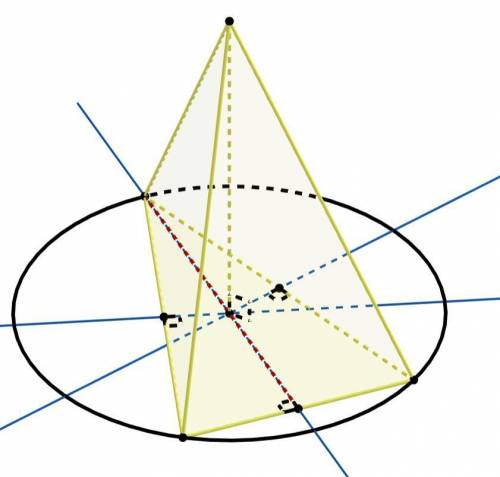
Если боковые рёбра пирамиды составляют равные углы с плоскостью основания, то основанием высоты пирамиды является центр окружности описанной около многоугольника из основания.
Центр окружности описанной около треугольника лежит внутри треугольника, если он остроугольный.
Так же этот центр лежит на пересечении серединных перпендикуляров к сторонам треугольника. Если центр описанной окружности лежит на одной высоте треугольника, то эта высота лежит на серединном перпендикуляре. А значит высота одновременно является и медианой. Тогда треугольник равнобедренный.
Около любого треугольника можно описать единственную окружность. Стороны треугольника - хорды этой окружности и делят ее на три части. Если взять точку D на дуге АВ, стягиваемой хордой АВ и провести из этой точки хорды DE или DF, не проходящие через точки А и В соответственно и через точку С (оговорено в условии), то эти хорды пересекут хорду АВ и дугу АС или ВС соответственно, а значит и хорды АС или ВС, стягивающие эти дуги. Так как через две точки можно провести только одну прямую, точку D можно взять в любом месте на прямых, содержащих хорды DE или DF.
Объяснение: