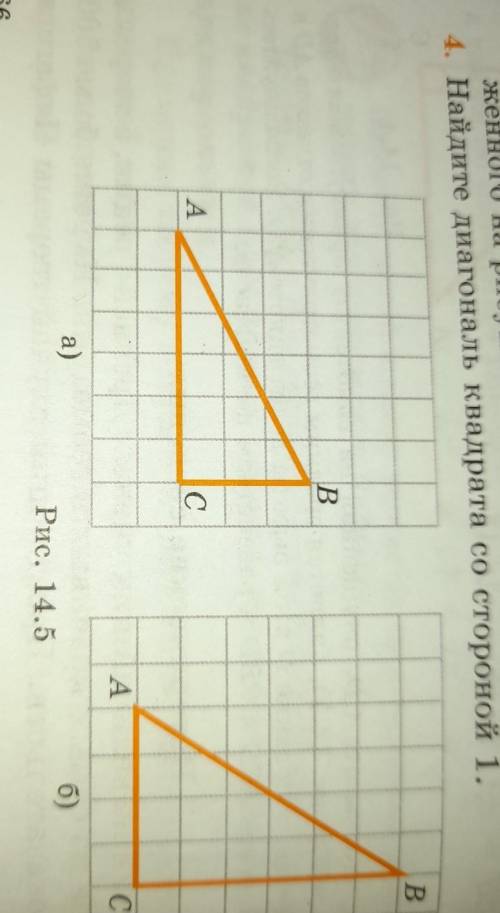
На стороне ВС параллелограмма ABCD отмечена такая точка М, что ВМ : МС = 1 : 3. Чему равна площадь треугольника АВМ, если площадь параллелограмма равна S?
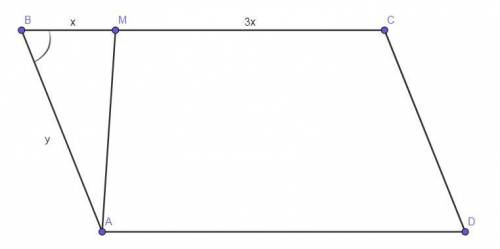
Чертёж смотрите во вложении.
Дано:
Четырёхугольник ABCD - параллелограмм.
Точка М ∈ ВС.
ВМ : МС = 1 : 3.
S(ABCD) - S.
Найти:
S(ΔАВМ) = ?
Пусть ВМ = х, тогда МС = 3х, АВ = у. Площадь ΔАВМ обозначим как S₁.
Площадь параллелограмма равна произведению смежных сторон и синусу угла между ними.
Следовательно -
S(ABCD) = ВС*АВ*sin (∠В)
ВС = ВМ+МС = х+3х = 4х.
То есть -
S = 4ху*sin (∠В)
Рассмотрим ΔАВМ.
Площадь треугольника равна половине произведения смежных сторон и синуса угла меду ними.
То есть -
S(ΔАВМ) = 0,5*ВМ*АВ*sin (∠В)
S₁ = 0,5*хy*sin (∠В).
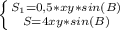
Из первого уравнения системы следует, что -
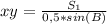
Подставим это значения во второе уравнение системы -
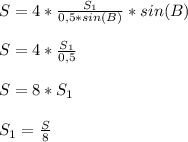
S(ΔАВМ) = S(ABCD)/8
S(ΔАВМ) = S/8.
ответ: S/8.
ответ: 20 см
Решение: смотри рисунок.
Пусть треугольник BAC равнобедренный, AB=AC=10 см.
Возьмем произвольную точку K на основании BC и проведем KM||AC иKN||AB
KM=AN, KN=AM -противоположные стороны параллелограмма.
Докажем, что KM=BM. Угол 2=углу 4 как соответственные углы при AC||KM и секущей KC. Но угол 4=углу 1 (углы при основании равнобедренного треугольника). Отсюда угол 2=углу 1. Значит треугольник BMK равнобедренный и KM=BM как его боковые стороны.
Аналогично докажем, что KN=NC. Угол 3=углу 1 как соответственные углы при AB||KN и секущей KB. Но угол 1=углу 4 (углы при основании равнобедренного треугольника). Отсюда угол3 =углу 4. Значит треугольник KNC равнобедренный и KN=NC как его боковые стороны.
Периметр параллелограмма =KM+MA+AN+NK=BM+MA+AN+NC=BA+AC=10+10=20 (см)