Один из углов ромба равен 120 градусов. точка пересечения диагоналей ромба удалена от стороны ромба - id151027820200808 от bohdan4ever 08.08.2020 23:28

Question

Геометрия: Один из углов ромба равен 120 градусов. точка пересечения диагоналей ромба удалена от стороны ромба на 2корня из 3 см. найти периметр ромба.

bohdan4ever · Accepted Answer

а) (-2;0) - центр окружности, радиус окружности равен 3.

б) (0; 4) - центр окружности, радиус окружности равен 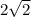$2\sqrt{2}$ .

в) (5; -7) - центр окружности, радиус окружности равен 4.

Объяснение:

Уравнение окружности имеет вид: (x-a)²+(y-b)²=R². Здесь центр окружности (a; b) . R - радиус окружности.

а) (-2; 0) -центр окружности, R²=9. R²=3². R=3.

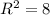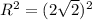
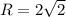б) (0; 4) - центр окружности, R^2=8 , $R^2=(2\sqrt{2})^2$ $R=2\sqrt{2}$ .

в) (5; -7) - центр окружности, R²=16, 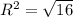$R^2=\sqrt{16}$ , R=4.

Заметим, что по условию задачи радиус всегда должен быть положительным. То есть при извлечении корня выбираем только арифметический корень

Один из углов ромба равен 120 градусов. точка пересечения диагоналей ромба удалена от стороны ромба на 2корня из 3 см. найти периметр ромба.

MOGZ ответил