24 см
Объяснение:
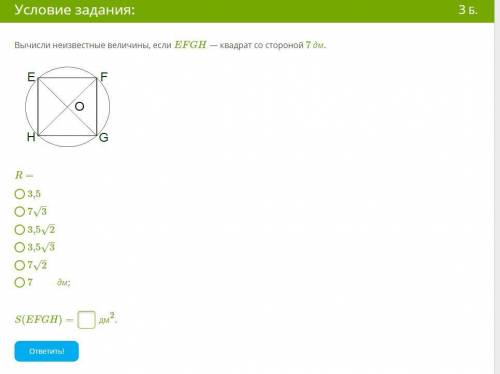
Дано: ΔАВС - прямокутний, ∠А=90°, ВС-АВ=4 см, АС=12 см. ВМ=АМ=СМ=26 см. МН⊥АВС. МН - ?
Якщо точка М віддалена на однакову відстань від усіх вершин ΔАВС, значить, точка Н знаходиться у центрі описаного кола. Центр описаного кола у прямокутного трикутника знаходиться посередині гіпотенузи.
Знайдемо гіпотенузу ВС за теоремою Піфагора:
ВС=х см, АВ=х-4 см
х²=(х-4)²+АС²
х²=х²-8х+16+144
8х=160; х=20
ВС=20 см.
ВН=СН=АН=20:2=10 см (це радіуси описаного кола)
Розглянемо ΔАМН - прямокутний.
МН=√(АМ²-АН²)=√(676-100)=√576=24 см
Площадь трапеции равна произведению полусуммы оснований на высоту, в данном случае это
(29 + 15) * 15 / 2 = 44 * 15 / 2 = 22 * 15 = 330 сантиметров квадратных
Так как верхнее основание (BC) и боковая сторона (CD) равны, то трапецию можно разделить на треугольник и квадрат. Площадь квадрата равна верхнему основанию трапеции, умноженному на боковую сторону, а площадь треугольника (он будет прямоугольным, так как высота, опущенная из точки B к нижнему основанию перпендикулярна этому основанию) будет равна половине произведения катетов. Катет BH (высота) нам известен, и он равен 15, второй катет мы найдём из разности оснований трапеции 29 - 15 = 14 сантиметров. Площадь треугольника равна 14 * 15 / 2 = 7 * 15 = 105 сантиметров квадратных, а площадь квадрата равна 225 сантиметров квадратных. Сложим вместе площади фигур и получим площадь трапеции, которая равна 105 + 225 = 330 квадратных сантиметров
Post Scriptum - это решение верно, только, если у трапеции сторона CD перпендикулярна нижнему основанию!