1. Дан равнобедренный треугольник с = и угол = 36°. Длина биссектрисы, проведенной из вершины , равна 10. Найдите длину высоты, проведенной из вершины .
1. Площади подобных треугольников относятся как квадрат коэффициента подобия.
Т.к. стороны A₁ B₁ C₁ в 2 раза меньше сторон ABC, то коэффициент подобия равен 2, =>
(см²)
2) Пусть сторона большого куба равна , тогда по условию сторона меньшего куба равна .
Объем большого куба: (см³)
Объем меньшего куба: (см³)
3) Матрешку можно рассматривать как цилиндр.
Формула массы цилиндра: - плотность материала, - объем цилиндра.
Формула объема цилиндра: - радиус основания, - высота цилиндра.
Если меньшая матрешка вдвое меньше большей, то делаем вывод что высота большей матрешки вдвое больше высоты меньшей матрешки, а также радиус основания большей матрешки вдвое больше радиуса основания меньшей матрешки.
Пусть - радиус основания меньшей матрешки, - высота меньшей матрешки, тогда по формуле:
Если ∠В=150°, то ∠А=180°-∠В=180°-150°=30° диагонали АС и BD-пересекаются под прямым углом и делят ромб пополам, то есть АС и BD-биссектрисы, значит О-центр круга и ∠ВАО=30°/2=15° проведем радиус в точку касания Н. (радиус проведенный в точку касания перпендикулярен самой касательной) Значит ОН также является высотой ΔАВО проведенной из прямого угла АОВ, следовательно ΔАНО подобен ΔОНВ, ∠BAO=∠HOB=15° (ЕСЛИ ТЕКСТ НИЖЕ ПОЛНОСТЬЮ НЕ ОТОБРАЖАЕТСЯ, ТО ПОСМОТРИ СКРИН)
Площадь любого многоугольника в который можно вписать в окружность находится по формуле:
1) 25
2) 15,625
3)1,2
Объяснение:
1. Площади подобных треугольников относятся как квадрат коэффициента подобия.
Т.к. стороны A₁ B₁ C₁ в 2 раза меньше сторон ABC, то коэффициент подобия равен 2, =>
2) Пусть сторона большого куба равна , тогда по условию сторона меньшего куба равна
, тогда по условию сторона меньшего куба равна 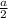 .
.
Объем большого куба: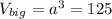 (см³)
(см³)
Объем меньшего куба: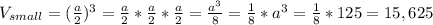 (см³)
(см³)
3) Матрешку можно рассматривать как цилиндр.
Формула массы цилиндра: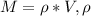 - плотность материала,
- плотность материала, 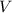 - объем цилиндра.
- объем цилиндра.
Формула объема цилиндра: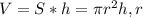 - радиус основания,
- радиус основания, 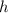 - высота цилиндра.
- высота цилиндра.
Если меньшая матрешка вдвое меньше большей, то делаем вывод что высота большей матрешки вдвое больше высоты меньшей матрешки, а также радиус основания большей матрешки вдвое больше радиуса основания меньшей матрешки.
Пусть - радиус основания меньшей матрешки,
- радиус основания меньшей матрешки, 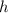 - высота меньшей матрешки, тогда по формуле:
- высота меньшей матрешки, тогда по формуле: