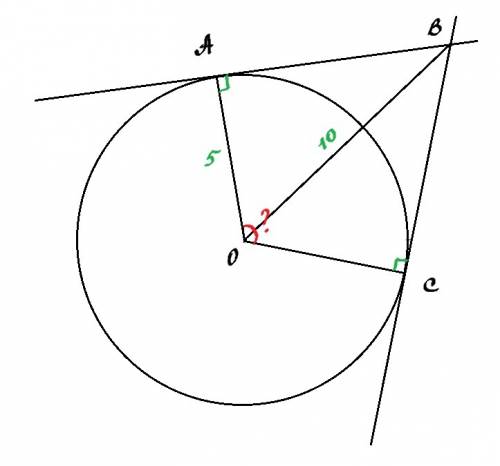
Рассмотрим ΔАВО. ОА - радиус окружности. ВА - касательная. Радиус окружности, проведенный в точку касания перпендикулярен касательной. Следовательно ΔАВО прямоугольный. ∠ОАВ = 90°.
ОА=5 - катет, ОВ = 10 - гипотенуза. Катет в два раза короче гипотенузы, следовательно он лежит напротив угла в 30°. Значит ∠АВО=30°, ∠АОВ=90°-30°=60°.
Рассмотрим ΔОВС. Он прямоугольный, т.к. радиус ОС проведен в точку касания, т.е. ОС⊥СВ. АО=ОС, т.к. являются радиусами окружности. ОВ - общая сторона треугольников АВО и ОВС. ΔАВО=ΔОВС по гипотенузе и катету.
Следовательно ∠АОВ=∠ВОС=60°.
∠АОС=∠АОВ+∠ВОС=60°+60°=120°.
ответ: ∠АОС=120°.
AB=CD=6 см, BC=AD=10 см (протвоположные стороны параллелограмма равны)
если точка H лежит на стороне AD, K на CD (рисунок)
Площадь параллелограмма равна произвеедению его стороны на высоту, опущенную на эту сторону
S=AD*BK=CD*BH
Отсюда BH=AD*BK/CD
BH=10*8/6=40/3 см=13 1/3 cм
если точка K лежит на стороне AD, H на CD (рисунок аналогичный только точки Н и К поменять местами)
Площадь параллелограмма равна произвеедению его стороны на высоту, опущенную на эту сторону
S=AD*BH=CD*BK
Отсюда BH=CD*BK/AD
BH=6*8/10=4.8 см