Объяснение:
Найдем гипотенузу АВ по Пифагору:
AB^2 = AC^2+BC^2 = 27+9= 36, отсюда гипотенуза АВ = 6
У описанной окружности, диаметром будет гипотенуза. Значит
радиус описанной окружности R=3
Радиус вписанной окружности r = (a+b-c)/2 = 1,5(
+1)-3 (a и b катеты, с - гипотенуза)
Против угла А лежит катет ВС, равный половине гипотенузы.
Значит <A = 30° а <B = 90°-30° = 60°
Сектор, содержащий хорду АС имеет угловую величину центрального угла АОС = 2-<B = 2*60 = 120°, значит площадь сектора в 3 раза меньше площади круга
S=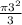
= 3π Отнимем отсюда площадь треугольника АОС и получим площадь сегмента
S(AOC) = 0,5S(ABC)=0,5*0,5*AC*BC = 0,25*3*3 = 2,25
S(сег) = S - S(АОС) = 3π - 2,25 = (π-2,25)
Объяснение:
Найдем гипотенузу АВ по Пифагору:
AB^2 = AC^2+BC^2 = 27+9= 36, отсюда гипотенуза АВ = 6
У описанной окружности, диаметром будет гипотенуза. Значит
радиус описанной окружности R=3
Радиус вписанной окружности r = (a+b-c)/2 = 1,5(+1)-3 (a и b катеты, с - гипотенуза)
Против угла А лежит катет ВС, равный половине гипотенузы.
Значит <A = 30° а <B = 90°-30° = 60°
Сектор, содержащий хорду АС имеет угловую величину центрального угла АОС = 2-<B = 2*60 = 120°, значит площадь сектора в 3 раза меньше площади круга
S=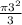 = 3π Отнимем отсюда площадь треугольника АОС и получим площадь сегмента
S(AOC) = 0,5S(ABC)=0,5*0,5*AC*BC = 0,25*3*3 = 2,25
S(сег) = S - S(АОС) = 3π - 2,25 = (π-2,25)
Поскольку ab||mn то ∠abm=∠bmn, как поскольку bn=nm то ∠bmn=∠mbn, как углы при основании из этого всего ∠mbn=∠bmn, тоэсть bm - бисектриса, которая в равнобедренном триугольнике есть и медианой ⇒ am=mc
ответ
ответ разместил: Гость
Решение и чертеж в приложении. ответ : r авс =5
ответ
ответ разместил: Гость
По теореме: если прямая, не проходящая ни через одну из вершин треугольника, пересекает одну из его сторон, то она пересекает только одну из двух других сторон. следовательно, не может.
ответ
ответ разместил: Гость
3. -3
Объяснение: