площадь ромбы вычисляется по формуле: a^2*sinA
у ромбы все стороны равны
также противоположные углы равны, следовательно, оставшиеся два углы = 360 - 150*2
угол 1 + угол 2=60
угол1=30, sin30 = 1/2
подставляем в формулу площади: 98 = a^2 *1/2
получается, что a=14
у ромбы 4 стороны, все равны, значит, периметр = 14*4= 56
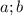. И пусть 
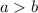тогда большая высота опускается на меньшую сторону , меньшая на большую . Тогда площадь с одной стороны равна 
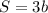, с другой стороны 
.
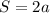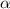тогда острый угол равен 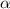следовательно тупой 
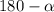. Из прямоугольных треугольников которые образовались после проведения высота соответственно на стороны 
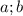равны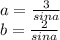 
тогда площадь запишится как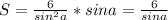 
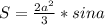приравняем 
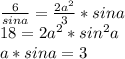-3 нам не подходит потому что синус в 
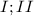четверти положителен 
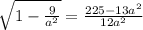решая это уравнение получим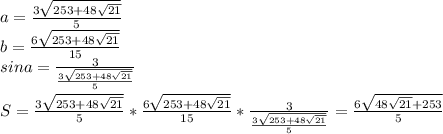 
S=a^2*sin 150 формула площади ромба
sin 150=sin(180-30)=sin 30=0,5
98=a^2*0,5
a^2=196
a=14
P=4*14=56