
Не знаю верно или нет ,но думаю так
Объяснение:
Если АD=AE , значит треугольник ADE равнобедренный
так же BD=EC и из этого следует , что AB=AC
значит ABC равнобедренный

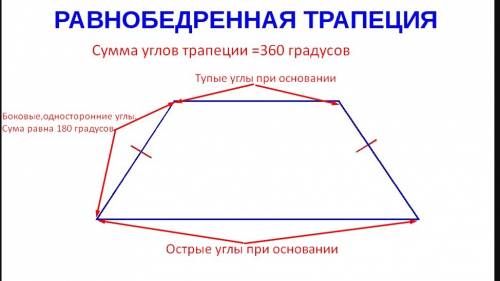
В равнобедренной трапеции боковые стороны равны,поэтому равны и углы при основаниях.Сумма боковых углов,односторонних равна 180 °,поэтому 268 °-это сумма тупых углов при основании.Сумма всех углов трапеции равна 360°.
Найти меньший угол трапеции можно двумя
1)Из суммы всех углов 360° вычесть суммы тупых углов 268° и разницу разделить на 2 (угла):
 °
°
2)Сумма боковых углов,односторонних равна 180 °,в условии-тупые углы при основаниях и их сумма равна 268°.
Один угол равен 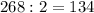 °.
°.
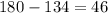 °-из суммы боковых углов вычли тупой угол.
°-из суммы боковых углов вычли тупой угол.
ответ:меньший угол трапеции равен 46 °.
Доказательство.
Так как AD = AE (по условию), то ΔADE равнобедренный. В равнобедренном треугольнике углы при основании равны.
∠ADE = ∠AED.
Если два угла равны, то смежные с ними углы тоже равны (так как сумма смежных углов равна 180°)
⇒∠ADB = AEC.
Тогда ΔADB = ΔAEC по первому признаку ( по двум сторонам и углу между ними).
AD = AE по условию; CE = DB по условию, ∠ADB = AEC по доказанному.
В равных треугольниках соответствующие стороны равны.
AB = AC ⇒ ΔABC равнобедренный.
Доказано.