a ∩ b.
Один из углов в 4 раза > другого.
Найти :Больший угол = ?
Решение :При пересечении двух прямых образуются четыре угла.
∠1 = ∠3, ∠2 = ∠4 (это пары вертикальных углов. Они равны между собой по свойству вертикальных углов).
Пусть ∠2 = х.
Тогда, по условию задачи, один из углов должен быть равен 4х.
Естественно, что ∠4 ≠ 4х, так как уже ∠4 = х по выше сказанному.
Тогда пусть ∠1 = 4х.
∠1 и ∠2 - смежные (по определению).
Сумма смежных углов равна 180°.Отсюда :
∠1 + ∠2 = 180°
4х + х = 180°
5х = 180° ⇒ х = 180° : 5 = 36°
4х = 4*36° = 144°.
(Естественно, что за 4х мы брали самый больший угол, поэтому в ответ пойдёт значение 4х).
ответ :144°.
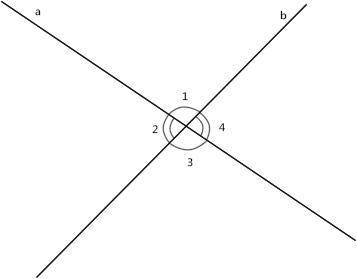
1)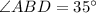 ; 2)
; 2)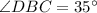
Объяснение:
Рассмотрим два решения (но при этом ответ не поменяется):
Обозначим данный угол буквами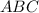 .
.
Проведём луч , перпендикулярный лучу
, перпендикулярный лучу 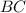 .
.
угол, образованный данными лучами с другой стороной угла -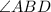 .
.
Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.Т.е.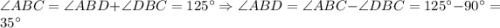
Обозначим данный угол буквами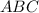 .
.
Проведём луч , перпендикулярный лучу
, перпендикулярный лучу  .
.
угол, образованный данными лучами с другой стороной угла -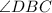 .
.
Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.Т.е.