Нет.
Объяснение:
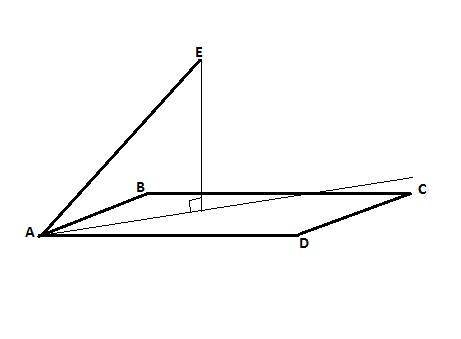
Прямые ЕА и ВС - скрещивающиеся прямые по определению:
"Две прямые называются скрещивающимися, если они не лежат в одной плоскости. Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости)".
В нашем случае прямая ВС лежит в плоскости АВСD, а прямая ЕА пересекает плоскость АВСD в точке А, не лежащей на прямой ВС.
Итак, прямые ЕА и ВС - скрещивающиеся прямые, поэтому через прямую АЕ и точки В и С нельзя провести плоскость.
P.S. Но через прямую ЕА и точку В, и через прямую ЕА и точку С можно провести две пересекающиеся плоскости, так как через три точки можно провести плоскость и при том единственную.
Объяснение:
а) Условие существования треугольника вытекает из теоремы о неравенстве треугольника. Чтобы треугольник существовал, необходимо, чтобы его большая сторона была меньше суммы двух других сторон.
Возьмем отрезки, равные 1см, 2см, 4см и 6см.
Из таких отрезков нельзя составить треугольник, так как
1+2 < 4, 1+2<6, 1+4<6, 2+4 = 6.
б) Цитата: "Для того, чтобы четырехугольник существовал, необходимо, чтобы длина одной из его сторон была меньше, чем сумма длин трех остальных сторон, иначе будет невозможно замкнуть периметр". Поэтому, если взять стороны 1см, 2см, 4см и 6см, то такой четырехугольник существует,но из его сторон в любой комбинации нельзя построить треугольник(доказано выше).