ответ: 39 (ед. площади)
Объяснение: Боковые ребра прямой призмы перпендикулярны основанию. Высота прямой призмы равна длине бокового ребра.
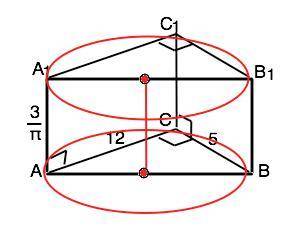
Отношение катетов ∆ АВС – АС:ВС=12:5, что указывает на то, что его стороны из Пифагоровых троек с отношением сторон 12:5:13. Гипотенуза АВ=13 (можно проверить по т.Пифагора).
. Гипотенуза АВ=13, она же - диаметр основания. => R=6,5, а высота цилиндра равна высоте призмы, т.е. длин Центром основания цилиндра, описанного около призмы, в основании которой прямоугольный треугольник, является середина гипотенузы. Гипотенуза AB=2R=d=13, высота цилиндра равна высоте призмы, т.е. длине её бокового ребра. Ѕ(бок. цил.)=π•d•h
Ѕ(бок)=π•13•3/π=39 (ед. площади).
AC = 10 см.
Объяснение:
A ---D--- C --- --- B
Т.к. точка C это середина отрезка AB, то AC=CB=1/2 от общей длины отрезка AB.
Т.к. точка D это середина отрезка AC, то AD=DC = (1/2) : 2 = 1/2 : 2/1 =1/2 * 1/2 = 1/4 от общей длины отрезка AB.
Из этого следует, что BD = 1/2 + 1/4 = 2/4 + 1/4 = 3/4 части отрезка AB и равна 15 см. AB=3/4=15см.
Соответственно AD = 1/4 части
3/4 = 15
1/4 = AD
AD = 1/4 * 15 : 3/4 = 15/4 : 3/4 = 15/4 * 4/3 = 15/3 = 5 см.
AB = AD + DB = 5 + 15 = 20 см
Длина отрезка AC = 20 / 2 = 10 см.
Диагональ АС параллелограмма АBCD равна 18см.Середина М стороны АВ соединена с вершиной D. Найдите отрезки, на которые делится диагональ АС отрезком DM.
Объяснение:
Проведем диагональ ВD, О-точка пересечения диагоналей . По свойству диагоналей параллелограмма АО=ОС=9 см.
Рассмотрим ΔАВD , АО-медиана ( тк. диагонали точкой пересечения делятся пополам) , MD- медиана ( т.к. М-середина по условию).
Пусть К-точка пересечения АО и МD.
По т. о точке пересечения медиан АО:КО=2:1 ⇒АО=9:3*2=6 (см)
Тогда КС=18-6=12 (см)
====================================
Медианы треугольника пересекаются в одной точке и делятся этой точкой на две части в отношении 2:1, считая от вершины.