Объяснение:
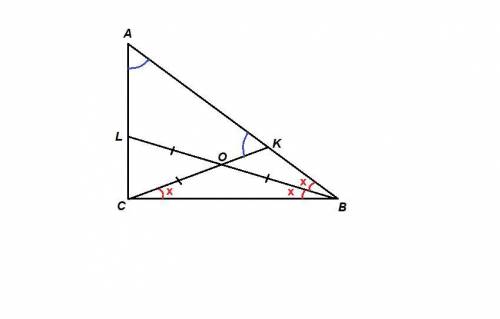
ΔLBC: ∠LCB = 90°, О - середина гипотенузы LВ, ⇒ СО - медиана, проведенная к гипотенузе, равна половине гипотенузы. Значит
ВО = OL = ОС.
Пусть половине угла В - х.
∠ОСВ = ∠ОВС = х, как углы при основании равнобедренного треугольника ОВС.
Тогда ∠АСК = 90° - х.
ΔАСК равнобедренный, так как СК = АС по условию, значит
∠САК = ∠СКА = (180° - ∠АСК) / 2 =
= (180° - (90° - x)) / 2 = (180° - 90° + x) / 2 = (90° + x) / 2
Сумма острых углов прямоугольного треугольника равна 90°:
∠САК + ∠АВС = 90°
Получаем уравнение:
(90° + x) / 2 + 2x = 90° | ·2
90° + x + 4x = 180°
5x = 90°
x = 18°
∠ABC = 2 · 18° = 36°
ABCD квадрат, точка м принадлежит стороне СD, MK ⊥( ABC), СМ = 4√2 см, MD = 8√2 см. Найдите расстояние между прямой МК и прямой: 1) АС; 2) BD.
Объяснение:
Расстояние между двумя прямыми - это наименьшее расстояние между любыми 2-я точками, лежащими на линии. Или между точкой лежащей на прямой с другой параллельной прямой.
1) Пусть МР⊥АС, тогда расстоянием между МК и АС будет отрезок МР. ΔСМР подобен ΔCDH по 2-м углам : ∠С-общий , ∠СРМ=∠COD=90° по св. диагоналей⇒ сходственные стороны пропорциональны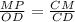
. Отрезок CD=4√2+8√2=12√2(cм) .
Найдем диагональ квадрата по т. Пифагора АС=√((12√2)²+(12√2)²)=24 ( см). Тогда половина диагонали DO=12 см.
2) Пусть МН⊥BD, тогда расстоянием между МH и BD будет отрезок МH. Т.к. MD=2/3*DC,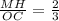
,