№1.
R - радиус описанной окружности, r - радиус окружности, вписанной в квадрат, а - сторона правильного шестиугольника, х - сторона квадрата, S - площадь круга.
R=a=20
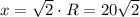
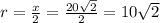
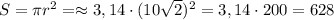
ответ: площадь круга, вписанного в квадрат, 628.
№2.
а - сторона правильного шестиугольника
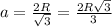
ответ: сторона правильного шестиугольника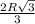 
.
№3.
Каждый из пяти углов правильного пятиугольника равен
.
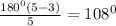Если провести две диагонали из одного угла, то они разделят пятиугольник на три треугольника. Рассмотрим два треугольника, в которых две из сторон являются сторонами исходного пятиугольника. Эти треугольники равны по первому признаку равенства треугольников, кроме того, они оба равнобедренные. Величина равных углов равна 
. Угол между диагоналями будет равен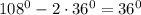 
ответ: угол между двумя диагоналями, проведенными из одной вершины правильного пятиугольника, равен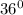 
.
1. Дано: правильная четырехугольная призма ABCDA₁B₁C₁D₁ и ...
-------------
B₁ D - ?
По условию задачи ABCD_квадрат и AA₁ ⊥ плоскости ABCD.
Из прямоугольного треугольника B₁C₁D:
* * * С₁D₁ проекция наклонной С₁D на плоскости A₁B₁C₁D₁ и B₁C₁ ⊥ С₁D₁ , следовательно по теореме трех перпендикуляров B₁C₁ ⊥ С₁D * * *
B₁ D= √(B₁C₁²+C₁C²)=√(6²+8²) =10 (см) . ответ: 1) 10 см
* * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * * *
2. Дано: правильная треугольная призма ABCA₁B₁C₁ ,
a=AB= AA₁=h =4 см . BN=BC/2 , B₁N₁=B₁C₁/2.
--------------------
S= S(AA₁N₁N) -?
Решение : Искомая сечения прямоугольник AA₁N₁N.
* * * т.к. BB₁C₁C_прямоугольник ⇒ BB₁N₁N тоже прямоугольник.
N₁N = BB₁ =AA₁=a , N₁N || BB₁ означает N₁N || AA₁ ) * * *
S =AN*NN₁
S = (a√3)/2* a =(a²√3)/2 = (4²√3)/2 =8√3 (см²). ответ: 8√3 см²
достаточно доказать, что в треугольнике abd угол bda > угол abdтогда против большего угла лежит большая сторона,ав > adугол bda равен углуdbc + угол bca ( внешний угол равен сумме внутренних, не смежных с ним)угол abd равен углу dbc ( bd – биссектриса)угол bda = угол abd + угол bca следовательно
угол bda > угол abd следовательно
ав > ad