Дано :
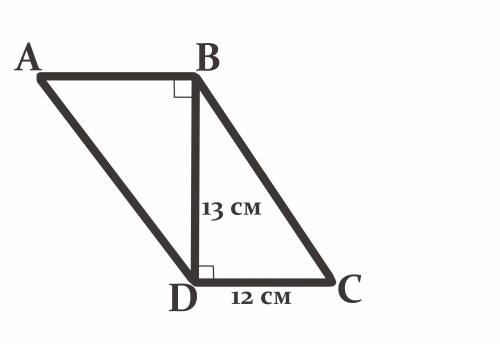
Четырёхугольник ABCD - параллелограмм.
Отрезок DB - диагональ = 13 см.
∠ABD = 90°.
CD = 12 см.
Найти :
S(ABCD) = ?
AB ║ CD (по определению параллелограмма).
Рассмотрим накрест лежащие ∠ABD и ∠BDC при параллельных прямых АВ и CD и секущей BD.
При пересечении двух прямых секущей накрест лежащие углы равны.То есть -
∠ABD = ∠BDC = 90°.
Тогда отрезок BD - ещё и высота параллелограмма ABCD (по определению).
Площадь параллелограмма равна произведению его стороны и высоты, опущенной на эту сторону.Следовательно -
S(ABCD) = BD*CD
S(ABCD) = 13 см*12 см
S(ABCD) = 156 см².
156 см².
1)BD высота по условию, значит в треугольник по одному равному углу. Сумма двух других углов=90 градусов. Если ∠CBD больше ∠ABD, то
∠C меньше ∠A⇒ CB больше AB.
2)В треугольнике ВМА угол ВАМ больше угла ВМА. (т.к. в любом треугольнике против большей стороны лежит больший угол и по условию ВМ>АВ)
Для треугольника ВМС угол ВМА является внешним и равен сумме внутренних углов треугольника ВМС, не смежных с ним. Т.е. угол ВМА больше угла ВСМ
Итак угол ВАМ > угла ВМА > угла ВСМ.
Значит, А > C.
3)Угол А в 2 раза меньше внешнего угла ВСК, то есть
∠А=α , ∠ВСК=2α.
Внешний угол треугольника = сумме двух внутренних углов, не смежных с ним. Значит, ∠ВСК=∠А+∠В ⇒ 2α=α+∠В ⇒ ∠В=α .
Получаем треугольник, у которого равны два угла, значит, треугольник равнобедренный ( углы при основании треугольника равны ).
4)7 треугольников
Объяснение: