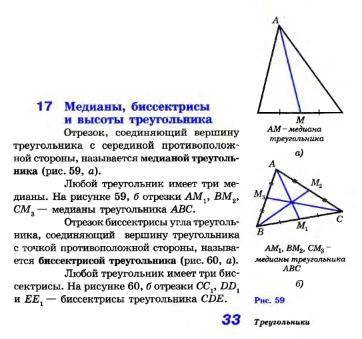
Медиана треугольника - отрезок, соединяющий вершину треугольника с серединой противоположной стороны. (рис, 59 а)
Биссектриса треугольника - отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны. (рис. 60 а)
Высота треугольника - перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону. (рис. 61)
Любой треугольник имеет:
· три медианы (рис. 59 б)
· три биссектрисы (рис. 60 б)
· три высоты (рис. 62 а, б, в)
Свойства:
- в любом треугольнике медианы пересекаются в одной точке.
- в любом треугольнике биссектрисы пересекаются в одной точке.
- в любом треугольнике высоты или их продолжения пересекаются в одной точке.

Sabcd = ah
MN║EF так как лежат на противоположных сторонах параллелограмма,
ME∦NF, ⇒ MNFE - трапеция, в которой
MN = 1/5 a, EF = 1/2 a, а высота так же h.
Smnfe = (MN + FE)/2 · h = (a/5 + a/2)/2 ·h = 7/10a / 2 · h = 7/20 ah
Sabcd : Smnfe = ah / (7/20 ah) = 20 : 7
ответ: D.