Пусть теорема имеет вид "если А, то В". Тогда обратная к ней будет иметь вид "если В, то А", а противоположная - "если не А, то не В". Противоположная теорема вовсе не является теоремой, потому что бессмысленна по своей сути.
Теорема №1:
Обратная (верна): Если все стороны параллелограмма попарно параллельны и равны, то такой параллелограмм является ромбом. Противоположная (не теорема): Если параллелограмм не является ромбом, то никакие из его сторон не равны и не параллельны.Противоположная обратной (не теорема): Если стороны параллелограмма не равны и попарно не параллельны, то такой параллелограмм не является ромбом.Теорема №2:
Это точно полная формулировка теоремы? Соответственные углы равны только при пересечении параллельных прямых секущей. Иначе это не верно. То есть, полная теорема звучит так: если две прямые пересечены секущей, то образованные соответственные углы равны.
Обратная (верна): Если соответственные углы равны, значит прямые параллельны.Противоположная (не теорема): Если две прямые не пересечены секущей, то образованные соответственные углы не равны.Противоположная обратной (не теорема): Если соответственные углы не равны, значит прямые не параллельны.
A(2;2) , B(6;6)
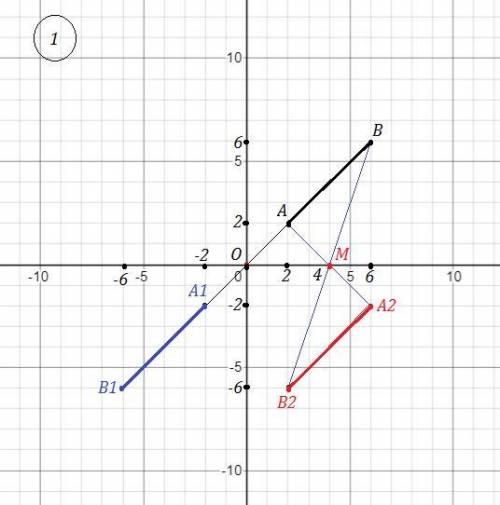
1) Чтобы начертить отрезок, симметричный отрезку АВ относительно точки О(0;0) , надо соединить точку О с точками А и В и отложить от точки О отрезки, равные ОА и ОВ . Получим отрезок А1В1 . Рис. 1 .
А1(-2;-2) , В1(-6;-6)
2) 1) Чтобы начертить отрезок, симметричный отрезку АВ относительно точки М(4;0) , надо соединить точку М с точками А и В и отложить от точки М отрезки, равные МА и МВ . Получим отрезок А1В1 . Рис. 1 .
А2(6;-2) , В2(2:-6)
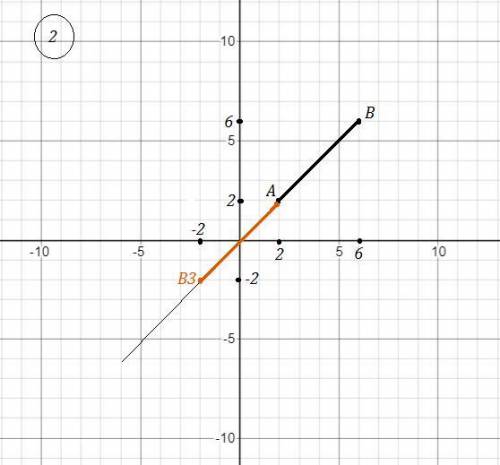
3) 1) Чтобы начертить отрезок, симметричный отрезку АВ относительно точки А(2;2) , надо продлить отрезок АВ и от точки А отложить отрезок, равный отрезку АВ . Получим отрезок АВ3 . Рис. 2.
А(2;2) , В3(-2;-2)
2) Конусы подобны, тогда радиусы их окружностей в основании относятся как:
, где 
- коэффициент подобия, тогда их высоты относятся как: 
или 
Тогда сечение делит высоту в отношении (От вершины конуса к основанию):
3) Расстояние от точки до отрезка - это перпендикуляр, опущенный из данной точки (O) на этот отрезок (АB). OH = 23 см (то самое расстояние), тогда OA=OB=r=34 см как радиусы одного шара.
По теореме Пифагора (ΔАOH):
AH=
см