Даны координаты вершин треугольника АВС Найти:
1) длину стороны АВ;
2) уравнения сторон АВ и АС и их угловые коэффициенты;
3) внутренний угол А;
4) уравнение высоты СD и ее длину;
5) уравнение и длину медианы АЕ;
6) уравнение окружности, для которой СD служит диаметром;
7) точку пересечения медиан;
8) уравнение прямой, проходящей через точку А, параллельно
стороне СD.
A (−2; 0)
B (1; 12)
C (7; 4)
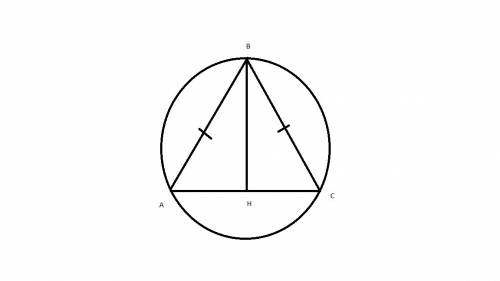
Доказательство. Пусть в треугольнике АВС сторона АВ больше стороны АС. Докажем, что угол С больше угла В. Для этого отложим на луче АВ отрезокAD, равный стороне АС. Треугольник АСD - равнобедренный. Следовательно, Ð1 = Ð2. Угол 1 составляет часть угла С. Поэтому Ð1 < ÐC. С другой стороны, угол 2 является внешним углом треугольника ВСD. Поэтому Ð2 > ÐB. Следовательно, имеем ÐC > Ð1 = Ð2 > ÐB.
Следствие: В произвольном треугольнике против большего угла лежит большая сторона.
Докажем, что если в треугольнике АВС угол С больше угла В, то и сторона АВ больше стороны АС. Действительно, эти стороны не могут быть равны, так как в этом случае треугольник АВС был бы равнобедренным и, следовательно, угол С равнялся бы углу В. Сторона АВ не может быть меньше стороны АС, так как в этом случае, по доказанному, угол С был бы меньше угла В. Остается только, что сторона АВ больше стороны АС.