Прямые BD и m - скрещивающиеся прямые.
Объяснение:
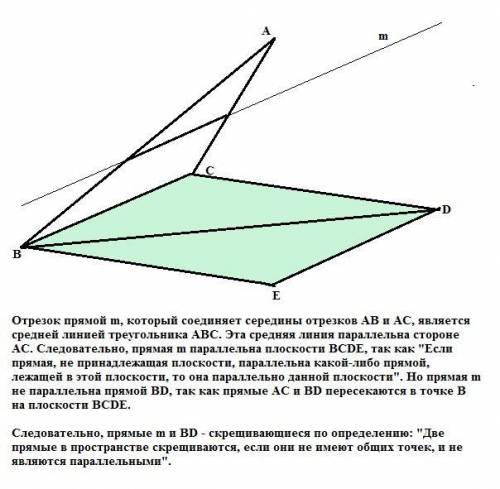
Отрезок прямой m, который соединяет середины отрезков AB и AC, является средней линией треугольника АВС. Эта средняя линия параллельна стороне АС. Следовательно, прямая m параллельна плоскости ВСDE, так как "Если прямая, не принадлежащая плоскости, параллельна какой-либо прямой, лежащей в этой плоскости, то она параллельно данной плоскости". Но прямая m не параллельна прямой BD, так как прямые АС и BD пересекаются в точке В на плоскости BCDE.
Следовательно, прямые m и BD - скрещивающиеся по определению: "Две прямые в пространстве скрещиваются, если они не имеют общих точек, и не являются параллельными".
Объяснение:
Периметр АDC=1,5 периметра АВС. Периметр АВС= 3 ВС=24 см.Периметр АDC,следовательно, равен 1,5•24=36 см. В то же время периметр АDC - это сумма длин боковых сторон (равных по условию) и длины основания. Значит, СD= (36-8)÷2= 14 см.