
Любое уравнение первой степени, имеющее вид Ax+By+C=0, где А, В, С – некоторые действительные числа (А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид Ax+By+C=0 при некотором наборе значений А, В, С.
Объяснение:
Доказательство
указанная теорема состоит из двух пунктов, докажем каждый из них.
Докажем, что уравнение Ax+By+C=0 определяет на плоскости прямую.
Пусть существует некоторая точка М0(x0, y0), координаты которой отвечают уравнению Ax+By+C=0. Таким образом: Ax0+By0+C=0. Вычтем из левой и правой частей уравнений Ax+By+C=0 левую и правую части уравнения Ax0+By0+C=0, получим новое уравнение, имеющее вид A(x-x0)+B(y-y0)=0. Оно эквивалентно Ax+By+C=0.
Полученное уравнение A(x-x0)+B(y-y0)=0 является необходимым и достаточным условием перпендикулярности векторов
→
n
=(A, B) и
→
M0M
=(x-x0, y-y0). Таким образом, множество точек M(x, y) задает в
Справочник
Прямая, плоскость
Статью подготовили специалисты образовательного сервиса Zaochnik.
Как работает сервис
Наши социальные сети
Общее уравнение прямой: описание, примеры, решение задач
Содержание:
Общее уравнение прямой: основные сведения
Неполное уравнение общей прямой
Общее уравнение прямой, проходящей через заданную точку плоскости
Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Составление общего уравнения прямой
Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.
Общее уравнение прямой: основные сведения
Пусть на плоскости задана прямоугольная система координат Oxy.
Теорема 1
Любое уравнение первой степени, имеющее вид Ax+By+C=0, где А, В, С – некоторые действительные числа (А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид Ax+By+C=0 при некотором наборе значений А, В, С.
Доказательство
указанная теорема состоит из двух пунктов, докажем каждый из них.
Докажем, что уравнение Ax+By+C=0 определяет на плоскости прямую.
Пусть существует некоторая точка М0(x0, y0), координаты которой отвечают уравнению Ax+By+C=0. Таким образом: Ax0+By0+C=0. Вычтем из левой и правой частей уравнений Ax+By+C=0 левую и правую части уравнения Ax0+By0+C=0, получим новое уравнение, имеющее вид A(x-x0)+B(y-y0)=0. Оно эквивалентно Ax+By+C=0.
Полученное уравнение A(x-x0)+B(y-y0)=0 является необходимым и достаточным условием перпендикулярности векторов
→
n
=(A, B) и
→
M0M
=(x-x0, y-y0). Таким образом, множество точек M(x, y) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора
→
n
=(A, B). Можем предположить, что это не так, но тогда бы векторы
→
n
=(A, B) и
→
M0M
=(x-x0, y-y0) не являлись бы перпендикулярными, и равенство A(x-x0)+B(y-y0)=0 не было бы верным.
Общее уравнение прямой: основные сведения
Следовательно, уравнение A(x-x0)+B(y-y0)=0 определяет прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение
A
x
+
B
y
+
C
=
0
определяет ту же прямую. Так мы доказали первую часть теоремы.
Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени
A
x
+
B
y
+
C
=
0
.
Зададим в прямоугольной системе координат на плоскости прямую
a
; точку
M
0
(
x
0
,
y
0
)
, через которую проходит эта прямая, а также нормальный вектор этой прямой
→
n
=
(
A
,
B
)
.
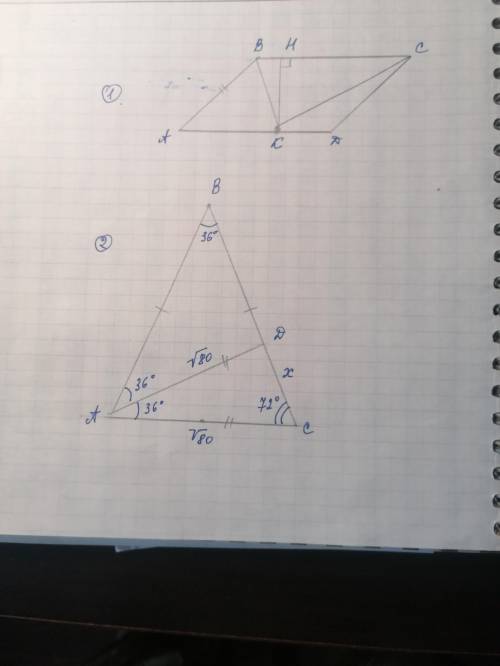
1. 108 см²
2. АВ=ВС=10+2√5; АС=4√5 (см рисунок)
Объяснение:
1.
У параллелограмма попарные стороны равны⇒АВ=СД=9 см, а АД=ВС
Биссектриса угла параллелограмма отсекает от него р/б Δ⇒
Биссектриса ∠В отсекла р/б Δ АВК ⇒АК=АВ=9 см
Биссектриса ∠С отсекла р/б Δ СДК ⇒КД=СД=9 см
АД=9+9=18 см
КH является высотой параллелограмма, т к точка К лежит на ВС. Расстоянием между параллельными прямыми называется расстояние от какой-нибудь точки одной прямой до другой прямой.
Можем посчитать площадь:
S=АД*КН=18*6=108 см²
2.
Обозначим Δ буквами АВС, где ∠В=36° (см рисунок) и АВ=ВС, и найдем два остальных угла р/б ΔАВС=(180-36)\2=72°
Биссектриса поделила ∠А пополам ⇒∠ВАД=∠ДАС=36°. Найдем ∠АДС=180-36-72=72°
Мы видим, что Δ САД подобен ΔАВС (по трем углам).
Выразим соотношение сторон: АС/ДС=ВС/АД
Возьмем СД за х, тогда АВ=ВС=√80+х:
√80/х=(√80+х)/√80⇒х(√80+х)=√80*√80=
х²+√х-80=0 Решим уравнение:
Дискриминант равен: (√80)²-4*1*(-80)=80+320=400=20²
Найдем корни:
***√80=√16*√5=4√5
X=(-√80+√20²)/2*1=(-√80+20)/2=(-4√5+20)/2=2(-2√5+10)/2=-2√5+10=10-2√5 - это ДС
Посчитаем все стороны ΔАВС:
АВ=ВС=4√5+(10-2√5)=4√5+10-2√5=10+2√5
АС=√80=4√5
1 дурыс это правдо верный ответ