Для того, щоб знайти абсцису (координату x) точки B, яка є одним із кінців відрізка AB, потрібно від подвоєної абсциси середини відрізка відняти абсцису іншого кінця відрізка:
xB=2xK-xA=2×0-2=-2;
Таким чином шукаємо й ординату (координату y) точки B:
yB=2yK-yA=1×2-4=-2
Відповідь: B(-2; -2).
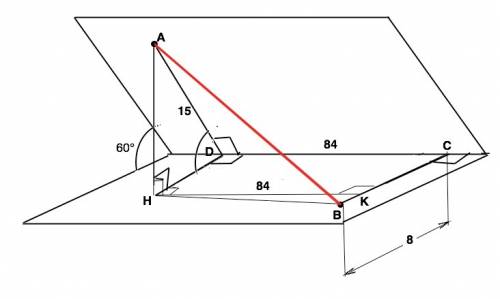
Опустим из т.А перпендикуляр АН на плоскость второй грани. Прямая, перпендикулярная плоскости, перпендикулярна любой прямой, лежащей в ней.
АН⊥НD. НD- проекция наклонной АD. По т. о 3-х перпендикулярах HD⊥DC, и АD⊥DC,⇒ угол АDH-равен углу данного двугранного угла, т.е. 60°.. Треугольник АНD – прямоугольный по построению. DН=АD•cos60°=7,5 см. АН=АD•sin60°=7,5√3 см. Проведем НК║DC. HD и ВС перпендикулярны CD. Четырехугольник ВСDH - прямоугольник, КС=HD=7,5 см. ⇒ ВК=ВС-КС=0,5 см. ∆ НКВ - прямоугольный ( угол К=90°). По т.Пифагора ВН²=HK²+BK²=84²+0,5²=7056.25. Так.как АН⊥ВН, из прямоугольного ∆ АНВ по т.Пифагора АВ=√(BH²+AH²)=√(7056.25+168,75)=85 см
xk=(xa+xb)/2 0=(2+xb)/2
yk=(ya+yb)/2 1=(4+yb)/2
xb=-2 yb=-2
B(-2;-2)