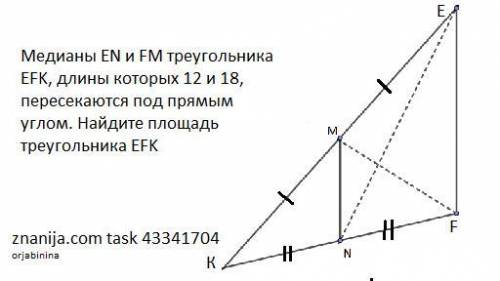
Медианы ЕN и FM треугольника EFK, длины которых 12 и 18, пересекаются под прямым углом. Найдите площадь Треугольника EFK.
Объяснение:
1) Рассмотрим выпуклый четырёхугольник EFNM у которого диагонали , по условию, взаимно- перпендикулярны .
Его площадь можно найти по формуле S = 1/2*d₁*d₂* sin (∠d₁d₂).
S(EFNM) = 1/2*12*18* sin 90°=108 ( ед²).
2) S(EFK)=S(EFNM)+S(MNK)
3) MN-средняя линия , тк M,N-середины сторон по определению медианы . По т. о средней линии треугольника MN║EF .
ΔEFK ∼ΔMNK по 2-м углам : ∠К -общий ,∠FEK=∠NMK как соответственные при MN║EF ,секущей ЕК ⇒ сходственные стороны
пропорциональны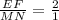 
, k=
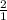. По т об отношении площадей
подобных треугольников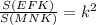 
или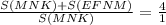 
,
4*S( MNK)=S(MNK)+S(EFNM) ,
3(MNK)=108 , S(MNK)=36 ед².
4) S(EFK)=S(EFNM)+S(MNK) =108+36=144 ( ед²).
Не верное утверждение Г.
Объяснение:
А) Прямоугольные треугольники с соответственно равными острыми углами (а даже и с одним, так как второй - прямой) ПОДОБНЫ. Отношение площадей подобных фигур равно квадрату коэффициента подобия (отношению линейных размеров). Значит отношение гипотенуз равно √(2/3). Утверждение верное.
Б) Диагональ трапеции делит ее на два треугольника с одинаковой высотой, следовательно их площади относятся, как их основания, к которым проведена эта высота. Утверждение верное.
В). Медиана треугольника делит треугольник на два треугольника, у которых равны и основания, и высоты. Значит и их площади равны. Утверждение верное.
Г). Периметры равновеликих треугольников в общем случае НЕ равны. (Предыдущий пример с медианой, когда треугольник не равнобедренный - периметры разные). Утверждение НЕ верное.