Впрямоугольнике abcd прямые m и n проходят через точку пересечения диагоналей. площадь фигуры, состоящей из трех закрашенных треугольников, равна 12 см квадратных. вычислите площадь прямоугольника abcd можно без
Медиана из вершины треголника делит противоположную сторону (основание) пополам. Высота из этого же угла перпендикулярна основанию. Треугольники, образовавшиеся при проведении высоты и медианы прямоугольные. У этих треуголников катеты образованные высотой и медианой равны. Катеты образованные делением основания медианой то же равны. Если катеты одного треугольника равны катетам другого треугольника, то такие треугольники равны. А значит боковые стороны исходного треугольника равны. Исходный треугольник равнобедренный.
Даны векторы k(-1;2), s(5;-12), c(2;x). Найдите: a)cos(∠k, s) ; b) число x, если k и c - коллинеарные; c) число x, если s и c - перпендикулярны.
Объяснение:
a)Косинус угла между векторами равен скалярному произведению этих векторов, деленному на произведение их длин.
Найдем длины векторов:
Длина вектора |k|=√( (-1)²+2²)=√(1 +4)=√5,
Длина вектора |s|=√( 5²+(-12)²)=√(25+144)=√169=13,
Скалярное произведение k*s=-1*5+2*(-12)=-5-24=-29
cos(∠k, s)= .
b) Два вектора коллинеарные ,если их координаты пропорциональны, значит для k(-1;2),c(2;x) :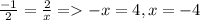 ;
;
c)Вектора перпендикулярны , если их скалярное произведение равно нулю : ⇒ 12x=10 , x=
⇒ 12x=10 , x=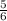 .
.