1. Построим полное сечение призмы плоскостью BDE1. Т.к. плоскость BDE1 пересекает параллельные плоскости ABCDEF и A1B1C1D1E1F1 по двум параллельным прямым, то ищем в плоскости A1B1C1D1E1F1 прямую параллельную BD и проходящую через точку E1.
Т.к. четырехугольник A1B1D1E1 - прямоугольник, то A1E1 || B1D1.
Т.к. четырехугольник BDD1B1 - прямоугольник, то BD || B1D1, откуда получаем, что A1E1 || B1D1.
Т.е. полным сечением призмы плоскостью BDE1 будет прямоугольник A1BDE1 (см. рис. 1)
Найдем проекцию прямой CC1 на плоскость A1BDE1. Для этого в плоскости A1B1C1D1E1F1 опустим перпендикуляр C1O1 на отрезок A1E1, а в плоскости ABCDEF опустим перпендикуляр CO на отрезок BD.
Продолжим прямые CC1 и OO1 до пересечения в точке G.
Угол C1GO1 (см. рис. 2) и будет искомым углом между прямой CC1 и плоскостью BDE1. Найдем его.
CO найдем из равнобедренного треугольника BCD, в котором он является высотой проведенной к основанию. Боковые стороны CB = CD = 1. Угол при вершине BCD = 120° (ABCDEF - правильный шестиугольник), а значит ∠DBC = ∠BDC = 30°, откуда CO = CB / 2 = 1/2.
C1O1 = C1H + HO1 = CO + D1E1 = 1/2 + 1 = 3/2
В треугольнике O1OH сторона OH = CC1 = 1, а HO1 = D1E1 = 1, значит он равнобедренный и прямоугольный, откуда ∠HOO1 = 45°
Т.к. ΔHOO1 подобен ΔO1GC1, то ∠O1GC1 = ∠HOO1 = 45°,
т.е. угол между заданной прямой и плоскостью равен 45°
2. Для того, чтобы найти угол между плоскостью CB1D1 и прямой AB, найдем угол между этой плоскостью и прямой C1D1 параллельной прямой AB. (см. рис. 3)
Треугольник CD1B1 - равносторонний, т.к. все его стороны являются диагоналями равных квадратов со стороной 1.
Точка C1 равноудалена от точек C, B1 и D1, а значит в правильной треугольной пирамиде C1CB1D1 (см. рис. 4) проекция точки C1 на основание CB1D1 попадет в центр описанной окружности ΔCB1D1.
В правильном треугольнике CB1D1 все стороны равны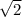 
(как диагонали квадратов со стороной 1). Радиус окружности описанной около равностороннего треугольника равен 
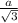, откуда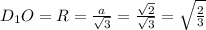 
Из прямоугольника тругольника C1OD1 найдем синус угла C1D1O, который и будет искомым:
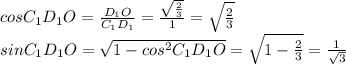
1. Построим полное сечение призмы плоскостью BDE1. Т.к. плоскость BDE1 пересекает параллельные плоскости ABCDEF и A1B1C1D1E1F1 по двум параллельным прямым, то ищем в плоскости A1B1C1D1E1F1 прямую параллельную BD и проходящую через точку E1.
Т.к. четырехугольник A1B1D1E1 - прямоугольник, то A1E1 || B1D1.
Т.к. четырехугольник BDD1B1 - прямоугольник, то BD || B1D1, откуда получаем, что A1E1 || B1D1.
Т.е. полным сечением призмы плоскостью BDE1 будет прямоугольник A1BDE1 (см. рис. 1)
Найдем проекцию прямой CC1 на плоскость A1BDE1. Для этого в плоскости A1B1C1D1E1F1 опустим перпендикуляр C1O1 на отрезок A1E1, а в плоскости ABCDEF опустим перпендикуляр CO на отрезок BD.
Продолжим прямые CC1 и OO1 до пересечения в точке G.
Угол C1GO1 (см. рис. 2) и будет искомым углом между прямой CC1 и плоскостью BDE1. Найдем его.
CO найдем из равнобедренного треугольника BCD, в котором он является высотой проведенной к основанию. Боковые стороны CB = CD = 1. Угол при вершине BCD = 120° (ABCDEF - правильный шестиугольник), а значит ∠DBC = ∠BDC = 30°, откуда CO = CB / 2 = 1/2.
C1O1 = C1H + HO1 = CO + D1E1 = 1/2 + 1 = 3/2
В треугольнике O1OH сторона OH = CC1 = 1, а HO1 = D1E1 = 1, значит он равнобедренный и прямоугольный, откуда ∠HOO1 = 45°
Т.к. ΔHOO1 подобен ΔO1GC1, то ∠O1GC1 = ∠HOO1 = 45°,
т.е. угол между заданной прямой и плоскостью равен 45°
2. Для того, чтобы найти угол между плоскостью CB1D1 и прямой AB, найдем угол между этой плоскостью и прямой C1D1 параллельной прямой AB. (см. рис. 3)
Треугольник CD1B1 - равносторонний, т.к. все его стороны являются диагоналями равных квадратов со стороной 1.
Точка C1 равноудалена от точек C, B1 и D1, а значит в правильной треугольной пирамиде C1CB1D1 (см. рис. 4) проекция точки C1 на основание CB1D1 попадет в центр описанной окружности ΔCB1D1.
В правильном треугольнике CB1D1 все стороны равны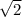
(как диагонали квадратов со стороной 1). Радиус окружности описанной около равностороннего треугольника равен 
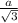, откуда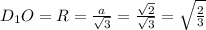 
Из прямоугольника тругольника C1OD1 найдем синус угла C1D1O, который и будет искомым: