ответ: 2688 см²
Объяснение:
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны.
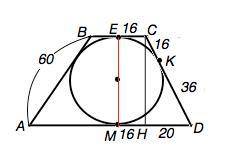
Для трапеции АВСD, в которую вписана окружность, BC+AD=AB+CD=60+16+36=112 см.
Стороны трапеции - касательные к вписанной окружности. Обозначим точки касания на ВС– Е, на СD - К, на AD-М. По свойству равенства отрезков касательных, проведенных из одной точки, СЕ=СК=16, DK=DM=36.
Соединим точки касания на основаниях отрезком ЕМ. Опустим высоту СН. МН=ЕС=16
DH=DM-CE=36-16=20.
По т.Пифагора СН=√(CD²-DH²)=√(52²-20²)=48 (см)
Площадь трапеции равна произведению полусуммы оснований на высоту.
S(ABCD)=0,5(BC+AD)•CH=0,5•112•48=2688 см².
1) Если все боковые стороны (это рёбра) пирамиды имеют одинаковую длину, то их проекции на основание - радиусы R описанной окружности вокруг основания.
Радиус равен половине диагонали основания.
R = √(3² + 4²) = 5 см.
Тогда высота Н пирамиды равна:
Н = √(13² - 5²) = √(169 - 25) = 12 см.
2) Будем считать, что в задании имеется в виду, что высота пирамиды проецируется на основание в вершину прямого угла.
Тогда 2 боковых грани пирамиды вертикальны, одна - наклонная.
Гипотенуза основания равна √(9² + 12²) = 15 см.
Высота основания на гипотенузу равна (9*12)/15 = (36/5) = 7,2 см.
Высота наклонной боковой грани равна √(8² + 7,2²) = 0,8√181 ≈ 10,7629 см.
Теперь можно определить площади боковых граней.
Sбок = (1/2) *(6*8 + 12*8 + 15*(4/5)√181) = (72 + 6√181) см².
Площадь основания Sо = (1/2)(9*12) = 54 см².
Полная площади пирамиды равна 54 + 72 + 6√181 = 126 + 6√181 см².
Объём пирамиды равен (1/3)*54*8 = 144 см³.
Объяснение:
100%