7. BM = (1/4)·(a+c) - b.
8. D = √13 ед.
Объяснение:
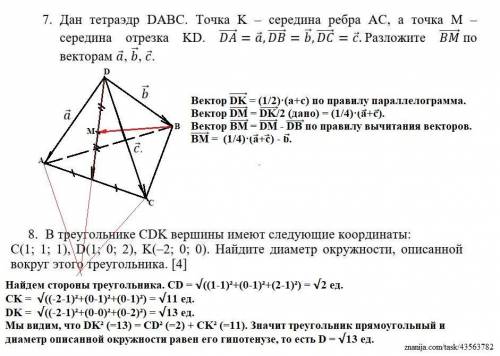
7. Вектор DK = (1/2)·(a+c) по правилу параллелограмма (АК=КС).
Вектор DM = DK/2 (дано) = (1/4)·(a+c).
Вектор ВМ = DM - DB по правилу вычитания векторов.
BM = (1/4)·(a+c) - b.
8. Найдем стороны треугольника. CD = √((1-1)²+(0-1)²+(2-1)²) = √2 ед.
CK = √((-2-1)²+(0-1)²+(0-1)²) = √11 ед.
DK = √((-2-1)²+(0-0)²+(0-2)²) = √13 ед.
Мы видим, что DK² (=13) = CD² (=2) + CK² (=11). Значит треугольник прямоугольный и диаметр описанной окружности равен его гипотенузе, то есть D = √13 ед.
Отношение сторон треугольника АВD- 12:16:20=3:4:5. Это отношение сторон "египетского" треугольника, значит, ∆ АВD- прямоугольный. (Можно проверить по т.Пифагора)
∆ ВСЕ - прямоугольный по построению, т.к. СЕ⊥BD.
ВС||AD, ⇒ ∠СВD=∠BDA как накрестлежащие. Если острый угол одного прямоугольного треугольника равен острому углу другого, они подобны.
∆ BEC ~ ∆ ABD.
Тогда ∠ВСЕ=∠ВАD, и их тригонометрические функции равны.
sin ВСЕ=sin A=BD/AD=16/20=0,8
cos ВСЕ=cos A=AB/AD=12/20=0,6
tg BCE=tg A=BD/AB=16/12=4/3

ответ: 30
Объяснение: По свойству: Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна 180∘
180-50=30