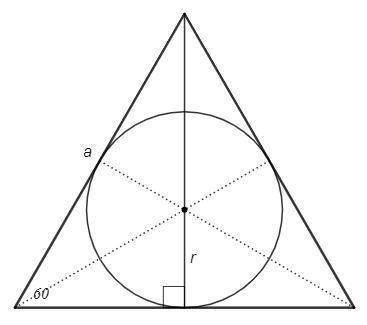
Центр вписанной окружности треугольника - точка пересечения биссектрис.
В равностороннем треугольнике все биссектрисы являются также высотами и медианами.
h =a*sin60 =√3/2 a
Медианы треугольника делятся точкой пересечения в отношении 2:1 от вершины.
r =1/3 h =√3/6 a
a =6/√3 r =6/√3 *4√3 =24
Или
Точка пересечения биссектрис - центр вписанной окружности (O).
В равностороннем треугольнике все биссектрисы являются также высотами и медианами.
OH=4√3 (радиус), AC=2AH
В треугольнике (AOH) с углами 30, 90 стороны относятся как 1 :√3 :2
(катет против угла 30 равен половине гипотенузы, далее по теореме Пифагора)
AH=OH*√3 => AC=OH*2√3 =4√3 *2√3 =24

3.
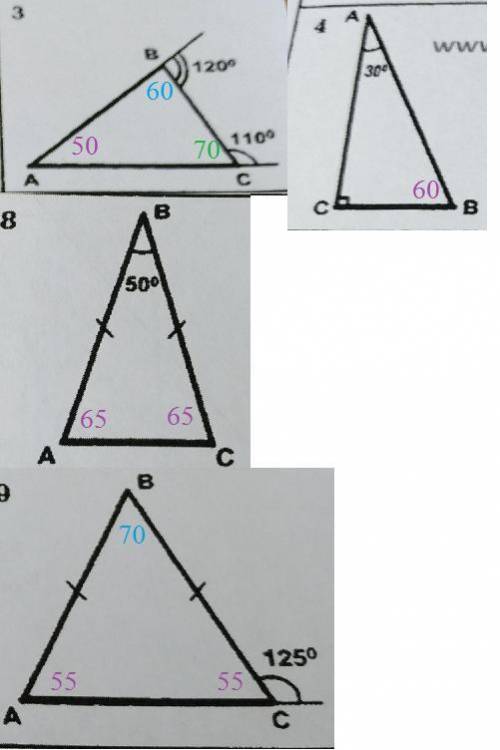
Cумма смежных углов 180 градусов.
Если один угол 120°, то второй 180°-120°=60°
Если один угол 110°, то второй 180°-110°=70°
Сумма углов треугольника АВС равна 180 градусов, два угла 60° и 70°, значит угол А равен 180°-60°-70°=50°
4.
Сумма острых углов прямоугольного треугольника равна 90°
Если один угол 30°, то второй 90°-30°=60°
8. Треугольник равнобедренный (АВ=ВС), значит углы при основании равны
Сумма углов треугольника равна 180°
180°-50°=130° - приходится на два угла при основании
130°:2=65°
9.
Cумма смежных углов 180 градусов.
Если один угол 125°, то второй 180°-125°=55°
Треугольник равнобедренный (АВ=ВС), значит углы при основании равны.
∠А=∠С=55°
Сумма углов треугольника равна 180°
180°-55°-55°=70° - третий угол треугольника
6,28 см
Объяснение:
1) Диаметр D окружности, описанной около квадрата равен диагонали d квадрата, которая может быть рассчитана по теореме Пифагора как сумма квадратов катетов, а катеты являются сторонами квадрата:
D = d = √ (√2)²+(√2)² = √ (2 +2) = 2 см.
2) Находим длину окружности:
L = π · D = 3,14 · 2 = 6,28 см
ответ: 6,28 см.