Противоположные углы параллелограмма равны. Углы, примыкающие к одной стороне - внутренние при пересечении параллельных прямых и секущей, их сумма равна 180°. ⇒
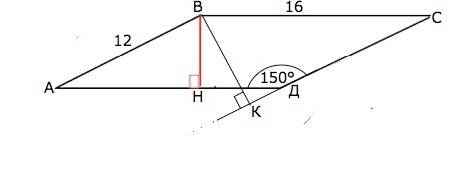
Угол ВАД=ВСД=180°-150°=30°.
Площадь параллелограмма равна произведению высоты на сторону, к которой проведена.
Высота ВН перпендикулярна стороне АД, ⇒∆ АВН - прямоугольный.
ВН противолежит углу 30° и равна половине гипотенузы АВ.
ВН=12:2=6 см.
S АВСД=ВН•АД=6•16=96 см²
Точно так же высота ВК, проведенная к СД, равна половине ВС, т.е. 8 см.
S АВСД=8•12=96 см²
Здесь в чертеже нужно достроить вторую высоту, получим два треугольника они прямоугольные и равнобедренные, острые углы у равнобедренных треугольников равны по 45 градусов, а раз два треугольника были одинаковы то и в одном и в другом углы будут по 45 градусов, если взять нижнее(большее) основание за AD, а верхнее(меньшее) BC, углы A и D будут равные, т.к. трапеция равнобедренная, и равны по 45 градусов, а углы B и С(верхнего основания) найдем через две параллельные и секущие. Пусть BC и AD параллельные BA секущая. Углы B и A односторонние, сумма их равна 180 градусов. через уравнение X+45=180 найдем угол B, X=180-45, X=135. Угол B=углуC=135 радусов.
ответ: угол A= углу D = 45 градусов, угол B = углу C = 135
:)
BC=AD
AB=CD( Свойство параллелограмма)
AP=QC
Рассмотрим треугольник АВС и треугольник АСD. Они равны так как у них две стороны равны, а сторона АС - общая.
Значит угол САD =углу ВСА
сторона АР=QC=BQ=PD.
Теперь рассмотрим два параллелограмма PQCD и АВQP
Они равны . Значит угол Р =углу В = углу D=углу Q. Отсюда следует , что треугольник АОР= треугольнику QOC . Отсюда следует , что сторона OP=OQ.
Что и требовалось доказать